Microscopic shell-model description of irrotational-flow dynamics in ¹⁰²Pd

In nuclear physics, two fundamental models of the nuclear structure exist. The first is the Bohr-Mottelson (BM) collective model [1], which is based on the quantization of the classical picture of surface vibrations and rotations of nuclear systems [2, 3]. For over fifty years, the understanding of quadrupole dynamics in atomic nuclei has been fundamentally shaped by three solvable limits within the BM collective model. These are 1) quadrupole vibrations of spherical nuclei; 2) rigid-flow rotations of strongly deformed nuclei, and 3) the γ-unstable rotor model applicable to transitional nuclei. These three types of quadrupole collectivity have been well conceptually described by the three exactly solvable limits of the BM collective model [1]. Developed in the early 1950s, this model continues to be a benchmark for comparing nuclear structures even today.

The second fundamental model is the nuclear shell model (see, e.g., [4]), which includes all many-particle fermion degrees of freedom and serves as a general microscopic framework in which other collective models can be founded. Many efforts have been made to establish the relationships between these two fundamental models of nuclear structure and to give the BM model a microscopic foundation, relating it to the nuclear shell model. In its standard formulation, however, the BM model cannot be naturally related to the microscopic shell-model theory. The solution has been provided through the algebraic approach by embedding the BM model in the shell model, i.e., by expressing it as a submodel of the shell model (see, e.g., [5, 6]). Recently, the BM model was embedded in the two-component proton-neutron shell-model theory within the framework of the proton-neutron symplectic model (PNSM) [7]. In the present study, the term "microscopic" implies that the collective model (in which the collective observables are expressed through the position and momentum coordinates of all the protons and neutrons that constitute the atomic nucleus) under consideration satisfy the Pauli principle and is a submodel of the nuclear shell model. One may alternatively refer to a model as semimicroscopic if it adheres to the Pauli principle but employs a phenomenological interaction. Such microscopic or semimicroscopic models are all shell-model submodels considered further.

The microscopic shell-model version [7] of the BM model has been successfully applied to the description of quadrupole dynamics in some strongly deformed [8], transitional [9], and weakly deformed [10] nuclei. In original BM [1] collective model, it is assumed that the quadrupole dynamics is of irrotational-flow type, which is actually related to the giant quadrupole resonance degrees of freedom. Indeed, the quadrupole vibrations of the nuclear surface within the BM model represent a high-energy collective mode, and the moments of inertia required to describe the experimentally observed low-energy rotational states are five times smaller than the irrotational-flow moments of inertia of the liquid drop values that the BM model predicts. This is not a problem because because in the practical application of the BM model, the moments of inertia are treated as free adjustable parameters. The question whether the quadrupole excitations of BM irrotational-flow type exist in some real nuclei is controversial, widely discussed, and still remains open.

The basic idea on the ground of the BM model is that the atomic nucleus is a deformable liquid drop and hence possesses a fundamental quantized surface vibrational mode of spherical equilibrium shape, since in this case there is no rotational degrees of freedom. The nature of vibrational states is directly associated with the form of the excitation quadrupole operator. Collective excitations, corresponding to the original BM irrotational-flow surface vibrations and rotations related to the giant resonance degrees of freedom, are represented within the PNSM by symplectic raising/lowering generators of $S p(12,R)$ dynamical algebra, cf. Eqs. (6) $ - $(7). These symplectic generators, in large-dimensional $S p(12,R)$ representations, contract [11] to the standard quadrupole phonon operators in the original BM model, and the traditional phonon scheme picture can be naturally obtained. Moreover, among $S p(12,R)$ algebra generators, beyond the quadrupole excitation operators of the low-energy rigid-flow rotations, there are the so called shear generators, which are the infinitesimal generators of irrotational-flow (sometimes also referred to as surface-wave) rotations. These shear operators, together with the rigid-flow angular-momentum operators, define some of the possible momentum operators of collective flows within the PNSM and close under commutation $S L(6,R)$ [10] $ - $ the group of volume preserving deformations and rotations in the six-dimensional collective space $ \mathbb{R}^{6} $. The later spaceis spanned by the microscopic proton-neutron quadrupole-monopole operators $ Q_{ij}(p,n) $ (cf. Eq. (1)), and they define the microscopic collective configuration space of the microscopic version of the BM model. The shell-model basis required for the description of the irrotational-flow quadrupole dynamics is provided in Ref. [10], where it was argued that a characteristic feature of this type of dynamics is almost linear monotonic increase in the $ B(E2) $ transition strengths between the states of the yrast band. In [10], as candidates that exhibit a quadrupole dynamics of BM irrotational-flow type were suggested $ ^{110} $Ru and $ ^{110} $Cd with experimentally measured intraband yrast $ B(E2) $ values of up to $ L = 6 $ and $ L = 8 $, respectively. However, in Ref. [12], the lifetime measurements of the yrast states up to $ L = 16 $ in $ ^{102} $Pd were reported. The extracted $ B(E2) $ transition probabilities for the yrast band in $ ^{102} $Pd exhibit such type of almost linear monotonic increase with respect to the angular momentum. The quadrupole excitations in the yrast band of $ ^{102} $Pd were even termed as "tidal waves" [12] and referred to as "quadrupole running waves on the surface of the nucleus" $ - $ in full accordance with the original BM model [2, 3] and its microscopic shell-model version [10]. The tidal-wave collective mode [12, 13] is expected to appear in vibrational or transitional nuclei and admits semiclassical interpretation within the microscopic self-consistent mean-field cranking approach, which allows to calculate the yrast energies and intraband $ B(E2) $ transisition probabilities. This, along the lines of Ref. [10], suggests $ ^{102} $Pd as a more pronounced candidate, exhibiting quadrupole dynamics of BM irrotational-flow type. Hence, the focus of this study is to examine the experimentally observed low-energy quadrupole dynamics in $ ^{102} $Pd within the microscopic shell-model version of the BM model. We restrict our considerations only to the low-energy collective states of the ground state (yrast) band and first two excited γ and β bands or quasibands.

The Pd isotopes are a typical example of transitional nuclei between spherical and γ-unstable nuclei. This is evident by the characteristic energy ratio $ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2.3 - 2.4 $, which is intermediate between that of spherical ($ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2 $−$ 2.2 $) and γ-unstable ($ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2.5 $) nuclei. With neutron number increasing from $ N = 50 $, quadrupole deformation increases from small values towards larger values in the middle of the shell. The two basic nuclear structures of spherical and γ-unstable nuclei are conceptually and quantitatively described well within the harmonic vibrator (HV) [2, 14] and the Wilets-Jean (WJ) γ-unstable [15] limits of the BM collective model [1].

The Pd isotopes were successfully described as transitional between $ U(5) $ and $ O(6) $ limits within the IBM-1 [16−20]. They were also analyzed within the affine $ SU(1,1) $ algebraic approach [21] used to describe the $ U(5)-O(6) $ transition. Furthermore, $ ^{102} $Pd is located approximately on the middle of the transition from $ U(5) $ to $ O(6) $, potentially very close to the $ E(5) $ critical point symmetry (CPS) [22], the latter possessing $ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2.20 $. It was even suggested as an $ E(5) $ nucleus in Ref. [23] based on the $ E_{4^{+}_{1}}/E_{2^{+}_{1}} $ energy ratio, the normalized $ B(E2; 4^{+}_{1} \rightarrow 2^{+}_{1}) $ and $ B(E2; 4^{+}_{2} \rightarrow 2^{+}_{2}) $ transition probabilities, and the reasonable agreement with $ 0^{+}_{3} $ properties identified with the $ 0^{+}_{\xi} $ state of the $ E(5) $ CPS. However, later, the more precise experimental data on the intraband $ B(E2) $ values for the yrast band up to $ L = 8 $ and the interband transitions have shown disagreement with the $ E(5) $ symmetry [24]. The nucleus $ ^{102} $Pd was on the focus in the paper by Frauendorf [25], in which its low-energy spectrum has been examined in detail within the framework of various nuclear structure models.

Collective observables of the proton-neutron symplectic model are provided by the following one-body operators [26]:

where $ i,j = 1,2,3 $; $ \alpha,\beta = p,n $; and $s = 1,2, \ldots, m=A-1$. In Eqs. (1)$ - $(4), $ x_{is}(\alpha) $ and $ p_{is}(\alpha) $ denote the coordinates and corresponding momenta of the translationally-invariant relative Jacobi vectors of the m-quasiparticle two-component nuclear system and A is the number of protons and neutrons.

The form of the $S p(12,R)$ generators (1)$ - $(4) directly reveals the dynamical content of the PNSM and physical significance of the symplectic generators. The 21 quadrupole operators $ Q_{ij}(\alpha,\beta) $ determine the shape and orientation of the proton/neutron subsystem and the nucleus as a whole. The 15 generators $ L_{ij}(\alpha,\beta) $ are the infinitesimal generators of $S O(6)$ group, which generate the low-energy rigid-flow rotations in abstract six-dimensional space. Among them, there are six components of standard three-dimensional angular momentum operators $ L_{ij}(p,p) $ and $ L_{ij}(n,n) $ ($ i\neq j $) of rigid-flow rotations of the proton and neutron subsystem, respectively. The remaining nine operators $ L_{ij}(p,n) $ represent the collective excitations of the combined proton-neutron system; cf. Eqs. (18) − (20). $ S_{ij}(\alpha,\beta) $ correspond to the 21 shear operators of infinitesimal shape change in the six-dimensional space, which together with operators $ L_{ij}(\alpha,\beta) $ generate $G L(6,R) -$ the group of deformations and rotations in six dimensions. The diagonal operators $ \{S_{ii}(p,p),S_{ii}(n,n), S_{ii}(p,n)\} $ are the infinitesimal generators of scale transformations (shape vibrations) along principal axis i. For instance, consider the operator $ S_{zz}(p,p) = \sum _{s}[x_{zs}(p)p_{zs}(p)+ p_{zs}(p)x_{zs}(p)] $, which using the standard Heisenberg-Weyl commutation relations and the expression $p_{zs}(p)= -{\rm i}\hbar\partial/\partial x_{zs}(p)$, takes the form $S_{zz}(p,p) = -{\rm i}\hbar[\sum _{s} 2x_{zs}(p)\partial/ \partial x_{zs}(p)+m]$. Then, the $ GL(1,R) \subset GL(6,R) $ group operator $\exp[{\rm i}\theta S_{zz}(p,p)]$ is a simple scaling operator along the z-axis of the proton subsystem, since ${\rm e}^{{\rm i}\theta S_{zz}(p,p)}\Psi_{p}(x_{xs}(p), x_{ys}(p),\,x_{zs}(p)) = \Psi_{p}(x_{xs}(p),\,x_{ys}(p),\,{\rm e}^{2\theta}x_{zs}(p))$ with $s= 1, 2,\ldots, m$. The same considerations are valid for other scaling operators. It should be observed that collective flows imply that group elements act uniformly on each many-particle coordinate. Monopole (breathing-mode) shape vibrations occur when scale transformations are equal along all three spatial directions: x, y, and z. Conversely, when deformations differ along these three spatial directions, they represent quadrupole shape vibrations in either proton, neutron, or a combined proton-neutron system. Hence, the off-diagonal operators $\{S_{ij}(p,p), S_{ij}(n,n),S_{ij}(p,n)\}$ ($ i\neq j $) represent the infinitesimal generators of irrotational-flow (surface-wave) rotations of the proton, neutron, and combined proton-neutron system, respectively, because a shape rotation is generated by continuously shrinking along one axis while at the same time expanding along another. Thus, an irrotational surface wave is generated, representing a shape rotation without any actual circulation of matter density. This is where the term 'irrotational-flow' (curl-free) rotation originates. In this way, the 36 operators of the group $G L(6,R) = \{L_{ij}(\alpha,\beta),\frac{1}{2}S_{ij}(\alpha,\beta)\}$ are obtained. They are the momentum operators, which generate different linear collective flows in nuclear system $ - $ i.e., the basic collective modes $ - $vibrational flows, rigid- and irrotational-flow rotations. When only the volume-preserving deformations and rotations are considered, i.e. excluding the monopole shape vibrations, one obtains the kinematical subgroup $S L(6,R) \subset G L(6,R)$. Finally, operators $ T_{ij}(\alpha,\beta) $ are the infinitesimal generators of monopole and quadrupole momentum tensor. Among them are the many-particle kinetic-energy operators of the proton, neutron, or combined proton-neutron system. For more details concerning the dynamical content of the PNSM, we refer the reader to Ref. [26].

The $S p(12,R)$ generators can be conveniently expressed in terms of the harmonic oscillator creation and annihilation operators

in the following $ O(m) $-invariant form [27]:

The operators (8), and (6)$ - $(7) are related to the proton-neutron valence-shell and giant resonance degrees of freedom, respectively.

In terms of operators (6)$ - $(8), the generators (1)$ - $(4) of the $S p(12,R)$ algebra become [27]

from which it is evident that shear operators $ S_{ij}(\alpha,\beta) $ are related with the giant-resonance irrotational-flow degrees of freedom.

The microscopic SM version of the BM model is defined by the following reduction chain [7]:

where the quantum numbers that characterize their irreducible representations are provided below for the different subgroups. The $S U(1,1)$ Lie algebra, related to the radial dynamics, is generated by the shell-model operators [7]:

which are obtained from (6)$ - $(8) by the contraction with respect to both indices i and α. The group $S O(6)$ can be expressed through the number-preserving $ U(6) $ generators $ A^{LM}(\alpha,\beta) $ (8) in the standard way by taking their antisymmetric combination [7]:

The generators of different $S O(6)$ subgroups along the chain (13) are provided by the following operators

and

which generate $S U_{pn}(3)$ and $S O(2)$ groups, respectively. The two groups $S U_{pn}(3)$ and $ S O(2) $, by construction, are mutually complementary [28] within the fully symmetric $ S O(6) $ irreps $ \upsilon \equiv (\upsilon,0,0)_{6} $ and form a direct product subgroup $ S U_{pn}(3) \otimes S O(2) \subset S O(6) $. Hence, $ S U_{pn}(3) $ irrep labels $ (\lambda,\mu) $ are in one-to-one correspondence with $ S O(6) $ and $ S O(2) $ quantum numbers υ and ν based on the following expression [7].

The reduction rules for $ S U_{pn}(3) \supset S O(3) $ are given in terms of a multiplicity index q, which distinguishes the same L values in the $ S U_{pn}(3) $ multiplet $ (\lambda,\mu) $ [29]:

According to the $S U(1,1) \otimes S O(6)$ structure, the microsopic quadrupole-monopole proton-neutron collective dynamics splits into radial and orbital motions. Then, the wave functions of the microscopic shell-model version of the BM model can be represented as products of radial functions and orbital $ S O(6) $ wave functions [7]:

where the orbital part $ Y^{\upsilon}_{\nu qLM}(\Omega_{5}) $ is presented by the $S O(6)$ Dragt's spherical harmonics [30, 31] and are characterized by $ S O(6) $ seniority quantum number υ.

A general shell-model Hamiltonian within the PNSM can be considered as

where $ H_{0} $ denotes the Harmonic oscillator Hamiltonian

and the collective potential $ V(Q) $ is a rotationally invariant function of the quadrupole operators (1) in the enveloping $S p(12,R)$ algebra. Thus, the collective potential $ V(Q) $ is a well-defined shell-model operator.

In the microscopic shell-model version of the BM model, the collective potential is as follows:

where $ q_{ij}={Q}_{ij}(p,n) $. Furthermore, $ V(q) $ is a rotationally invariant function that can be built up from different powers of the quadrupole moment operators $ q_{ij} $. However, since the potential $ V(\beta,\gamma) $ of the BM model can be expressed in terms of the microscopic quadrupole moment operators $ q_{ij} $, i.e. $ [q \times q]^{(0)} \sim \beta^{2} $ and $[q \times q \times q]^{(0)} \sim \beta^{3}\cos 3\gamma$, any BM Hamiltonian of the form

immediately defines a microscopic shell-model Hamiltonian

where operator $-\dfrac{\hbar^{2}}{2\mathfrak{B}}\nabla^{2}_{\rm Bohr}$ is replaced by the many-particle kinetic energy $ K(p,n)= \dfrac{1}{2M} \sum _{is}p_{is}(p)p_{is}(n) = \dfrac{1}{2M}T^{0}(p,n) $. A general Hamiltonian of the microscopic shell-model version of the BM model can therefore be expressed in the following form [32]:

Using the relation $ (\beta,\gamma) \leftrightarrow (\lambda,\mu) $ [33] and linear mapping of the rigid-rotor $ Rot(3) = \{L_{ij},q_{ij}\} $ algebra invariants to those of the $S U(3) = \{L_{ij},\widetilde{q}_{ij}\}$, the collective potential

can be represented in a much simpler form as follows:

In the present application, we use the following algebraic model Hamiltonian:

The dynamical symmetry Hamiltonian is chosen to be of the form:

where

and

It should be noted that the collective potential $V_{\rm coll}$ is of type (31). The first term in Eq. (33) represents the harmonic oscillator shell-model mean field that defines the shell structure, while $V_{\rm coll}$ in turn splits different $S U_{pn}(3)$ multiplets in energy. Furthermore, $ X^{a}_{3} \simeq [L\times Q^{a}\times L]^{(0)} $ and $ X^{a}_{4} \simeq [L\times Q^{a}\times Q^{a}\times L]^{(0)} $ terms with $ Q^{a}_{ij}\equiv \widetilde{q}_{ij} $ in Eq. (35) are the third- and fourth-order operators in $S U(3) \rightarrow S O(3)$ integrity basis $ \{C_{2}, C_{3}, L^{2}, X^{a}_{3}, X^{a}_{4}\} $ [34, 35], representing a part of the residual rotor Hamiltonian. Furthermore, we indicate that the Hamiltonian $H_{\rm SM} = H_{0} + H_{\rm res} \equiv H_{0} + aL^{2}+bX^{a}_{3}+cX^{a}_{4}$ actually represents a shell-model image of the rotor model Hamiltonian $H_{\rm rot} = A_{1}I_{1} + A_{2}I_{2} + A_{3}I_{3}$ [36] (see also, e.g., Ch. 7 of [37]), which additionally provides a physical significance to the high-order operators in the $ S U(3) \rightarrow S O(3) $ integrity basis.

Usually, in contrast to the present application, the shell-model image $H_{\rm SM}$ of the rotor-model Hamiltonian was used in practical calculations for a single $S U(3)$ irrep, for which the rigid-rotor collective dynamics is mapped to the shell-model fermion dynamics. Further, it is known that the $ X^{a}_{3} $ and $ X^{a}_{4} $ operators introduce an odd-even staggering in the γ band of γ-rigid type [36]. In Ref. [10], however, it was shown that by modifying them, it is possible to produce a γ-soft odd-even staggering pattern for the states of the γ band, which is a characteristic of the γ-unstable WJ model (see Figs. 1 and 4 for $ ^{102} $Pd). Thus, based on [10], we use the following parametrization $ c\equiv c(1-(-1)^{L}/\sqrt{2}) $ for the model parameter in front of the last term in Eq. (35).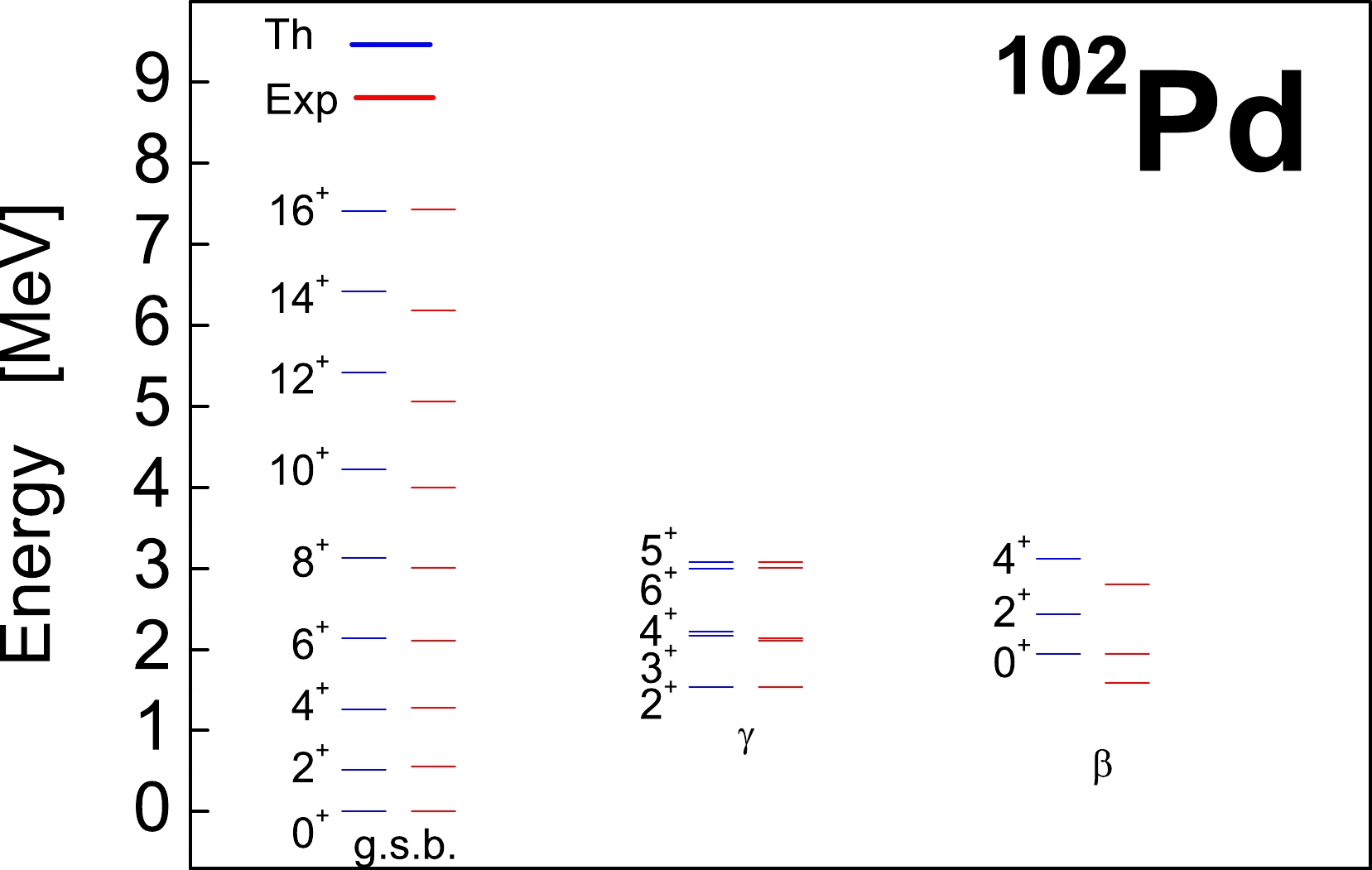

Figure 1.  (color online) Comparison of the excitation energies of ground, γ, and β bands in $ ^{102} $Pd with those obtained via experiment.

Figure 4.  (color online) Comparison of the experimental and theoretical staggering function $ S(L) $ (42) for the states of the γ band in $ ^{102} $Pd.

In Ref. [12], it has been demonstrated that the quadrupole motion of the tidal wave is marked by a significant increase in quadrupole deformation (and consequently, the moment of inertia) as angular momentum L increases within the yrast band. This is in contrast to strongly deformed nuclei with well-established rotational bands, where deformation and hence moment of inertia remain approximately constant. To address the observed increase in the moment of inertia, various expressions for spin- and energy-dependent inertia parameters have been employed in the literature. For instance, in Ref. [38], a two-parameter "soft-rotor formula"

was proposed for the excitation energies in the transitional nuclei with the moment of inertia $ \mathcal{J}=\mathcal{J}_{0}(1+\alpha L+\beta E_{i}) $, where $ E_{i} $ denotes the excitation energy of the corresponding bandhead of β and γ bands.

In Ref. [25], it was demonstrated that tidal wave energies of the yrast band for transitional nuclei can be described by the following expression:

where the moment of inertia depends linearly on L and is given by $ \mathcal{J}=\Theta_{0}+\Theta_{1}L $. This energy expression is obtained by the standard BM Hamiltonian, in which only the $S O(3)$ kinetic energy term is maintained. In Ref. [32], it was demonstrated that the standard BM Hamiltonian can be obtained as a contraction limit of the microscopic many-particle nuclear Hamiltonian. Alternatively, this can be realized by restricting the latter to the scalar $ O(m) $ irreducible collective space of the microscopic shell-model version of the BM model within the proton-neutron shell-model approach. Thus, by replacing the full many-particle kinetic energy in Eq. (28) with only its $S O(3)$ components (cf. [32]), our model Hamiltonian (33) will produce energies of the type (37). Additionally, considering spin-dependent moment of inertia $ \mathcal{J}=\Theta_{0}+\Theta_{1}L $, we can describe the tidal wave energies of the yrast band, as pointed in Ref. [25]. Thus, to account for the observed moment of inertia, we follow Refs. [25] and [38] and use a spin-dependent inertia paramater of the type $ a\equiv \dfrac{1}{2(\eta_{0}+\eta_{1}L)} $. Similar parametrization is used in Ref. [39], where the five-dimensional collective Hamiltonian, based on the relativistic covariant density functional theory, is applied to the yrast band tidal-wave collective mode in $ ^{102} $Pd.

The components of excitation operator are selected to be of the form [10]:

which are precisely the infinitesimal generators of irrotational-flow (surface-wave) rotations and $a^{\dagger}_{j}= \dfrac{1}{\sqrt{2}} \big(-{\rm i} B^{\dagger}_{j}(p)+B^{\dagger}_{j}(n)\big)$ with $ (a^{\dagger}_{j})^{\dagger}=a_{j} $ [40]. The normalization factor $ 1/2 $ in front of $ S^{2m}(a,a) $ operators in Eq. (38), which in Ref. [10] was included in the definition of the $S L(6,R)$ generators $ S^{2m}(\alpha,\beta) $, originates from the form of the quadrupole operators $ Q^{2m}(\alpha,\beta) = Q^{2m}_{su(6)}(\alpha,\beta)+ Q^{2m}_{sl(6,R)}(\alpha,\beta) $ with $ Q^{2m}_{su(6)}(\alpha,\beta) = \sqrt{3}A^{2m}(\alpha,\beta) $ and $ Q^{2m}_{sl(6,R)}(\alpha,\beta)= \dfrac{1}{2}(i)\sqrt{3}[F^{2m}(\alpha,\beta) -G^{2m}(\alpha,\beta)] \equiv \dfrac{1}{2}S^{2m}(\alpha,\beta) $. The latter ensures the self-consistent form of the full set of $S p(12,R)$ algebra generators.

The shell-model considerations, based on the proxy-$ S U(3) $ scheme [41, 42] provide the $ S p(12,R) $ irreducible representation 0p-0h $ [24]_{6} $ for $ ^{102} $Pd, which is fixed by the leading proxy-$ S U(3) $ irrep $ (18,6) $. The relevant irreducible collective space for $ ^{102} $Pd, spanned by the $ S p(12,R) $ irreducible representation 0p-0h $ [24]_{6} $ and restricted solely to the fully symmetric $ U(6) $ irreps, is provided in Table 1. The $ S U(3) $ multiplet $(18,~6)$ is contained in the maximal seniority $ S O(6) $ irreducible representation $ \upsilon_{0}=24 $ of the $ S p(12,R) $ bandhead structure, defined by the minimal Pauli allowed number of oscillator quanta $ N_{0}=403.5 $. The latter also includes the zero-point motion, obtained by filling the Nilsson levels of the three-dimensional oscillator with protons and neutrons. Further, assuming a pure $ S U_{pn}(3) $ state and using the expression [43]:

N	$ \upsilon \backslash \nu $	$\cdots 26$	$24$	$22$	$20$	$\cdots$	$4$	$2$	$0$	$-2$	$-4$	$\cdots$	$-20$	$-22$	$-24$	$-26$		$ \cdots $
$ \ \vdots $	$\vdots $	$\ddots\; \vdots$	$\vdots$	$ \vdots $	$\vdots $	$ \vdots $	$ \cdots $	$\vdots $	$\vdots $	$\vdots $	$ \vdots $	$ \vdots $	$\cdots $	$\vdots $	$ \vdots$	$\vdots $		${\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} $
$N_{0}+2$	26	(26,0)	(25,1)	(24,2)	$(23,3)$	$\cdots $	$(15,11)$	$(14,12)$	$(13,13)$	$(12,14)$	$(11,15)$	$\cdots $	$(3,23)$	$(2,24)$	$(1,25)$	$(0,26)$
	24		$(24,0)$	$(23,1)$	$(22,2)$	$\cdots $	$(14,10)$	$(13,11)$	$(12,12)$	$(11,13)$	$(10,14)$	$\cdots $	$(2,22)$	$(1,23)$	$(0,24)$
	22			$(22,0)$	$(21,1)$	$\cdots $	$(13,9)$	$(12,10)$	$(11,11)$	$(10,12)$	$(9,13)$	$\cdots $	$(1,21)$	$(0,22)$
	$\vdots$				$\ \ \ \ \ \ \ \ \ddots $			$\ \ \ \ \ \vdots $	$\ \ \ \ \vdots $	$\ \ \ \vdots $			$ {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} $
	2							$\ \ (2,0)$	$\ (1,1)$	$(0,2)$
	0								$(0,0)$
$ N_{0}$	24		$(24,0)$	$(23,1)$	$(22,2)$	$\cdots $	$(14,10)$	$(13,11)$	$(12,12)$	$(11,13)$	$(10,14)$	$\cdots $	$(2,22)$	$(1,23)$	$(0,24)$
	22			$(22,0)$	$(21,1)$	$\cdots $	$(13,9)$	$(12,10)$	$(11,11)$	$(10,12)$	$(9,13)$	$\cdots $	$(1,21)$	$(0,22)$
	$\vdots$				$\ \ \ \ \ \ \ \ \ddots $			$\ \ \ \ \vdots $	$\ \ \ \\vdots $	$\ \ \ \ \vdots $			$ {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} $
	2							$\ (2,0)$	$\ (1,1)$	$\ (0,2)$
	0								$\ (0,0)$

Table 1.  Relevant $S O(6)$ and $S U_{pn}(3)$ irreducible representations, which are contained in the $S p(12,R)$ irreducible collective space $0p-0h [24]_{6}$ of $^{102}$Pd and obtained according to Eq. (21).

the quadrupole deformation of $(18,~6)$ irreducible representation of $ ^{102} $Pd can be readily obtained with value $ \varepsilon = 0.16 $. This is slightly smaller than the experimental value 0.20 [44]. The latter suggests that vertical mixing of different $S U(3)$ multiplets can be used within the $S p(12,R)$ irreducible collective space $0p-0h\; [24]_{6}$. Hence, we introduce additional vertical mixing Hamiltonian:

where $ \widetilde{q}^{2M}= \sqrt{3}[A^{2M}(a,a)-A^{2M}(b,b)] $ are the $ S U_{pn}(3) $ quadrupole operators [40]. $ H_{v\, \rm mix} $ mixes simultaneously different $ S O(6) $ and $ S U_{pn}(3) $ irreducible representations of the type $ (\upsilon)=(\upsilon_{0}+2k) $ and $ (\lambda_{0}+2k,\mu_{0}) $, respectively, where $ (\lambda_{0},\mu_{0})=(18,~6) $ and $ k=0, ~1, ~2, \ldots $, within the $ S L(6,R) $ multiplet built on $ \upsilon_{0}=24 $.

The basic matrix elements of $ Sp(12,R) $ generators along the chain (13), defining the microscopic shell-model version of the BM model, are provided in Ref.[40]. Specifically, the matrix elements of the tensor interaction $ A^{2}(\alpha,\beta)\cdot F^{2}(\alpha,\beta) \simeq [A^{2}(\alpha,\beta)\times F^{2}(\alpha,\beta)]^{\upsilon=2}_{\nu=\pm2q=1l=0m=0} $ were given. Using the technique of Ref.[40], the $ SO(3) $-reduced matrix elements of the interaction $ \widetilde{q}^{2}\cdot F^{2}(a,a)= \sqrt{\dfrac{3.5}{2}}[\widetilde{q}^{2}\times F^{2}(a,a)]^{\upsilon=2}_{\nu=2q=1l=0m=0} $ in Eq. (40) can be similarly obtained in Eq.(40):

where $ \sqrt{\Delta\Omega(\sigma n'E';nE)}=\sqrt{\Omega(\sigma n'E')-\Omega(\sigma nE)} $ and $ \Omega(\sigma nE)=\dfrac{1}{4}\sum _{a=1}^{6}[2E^{2}_{a}-n^{2}_{a}+ 14(E_{a}-n_{a})-2a(2E_{a}-n_{a})] $ [40, 45]. The matrix elements of $ H_{\rm res} $ (35) in an $ S U(3) \supset S O(3) $ basis are provided in Ref. [46]. Hence, we already have all the required computational pieces for performing shell-model calculations within the PNSM.

We diagonalize the model Hamiltonian (32) within the $ S L(6,R) $ irreducible collective space built on $ \upsilon_{0} = 24 $ up to energy $ 20 \hbar\omega $. The results for the excitation energies of the lowest ground, γ and β bands in $ ^{102} $Pd are compared with experimental data [23, 47] in Fig. 1. The values of the model parameters, obtained by fitting to the excitation energies and $ B(E2;2^{+}_{1} \rightarrow 0^{+}_{1}) $ transition strength, are: $ C = -0.3988 $, $ D=0.00017 $, $ b = -0.00039 $, $ c = 0.000129 $, $ \xi = -0.00123 $ (in MeV), and $ \eta_{0} = 3.57 $, $ \eta_{1} = 1.56 $ (in MeV$ ^{-1} $). The figure shows a good description of the energy levels of the three bands under consideration, including the strong odd-even staggering of γ-soft type between the states of the γ band. Furthermore, in Fig. 2, the theoretical predictions for the intraband yrast $ B(E2) $ transition strengths are compared with the experimental results [12] and some other nuclear models, whose data are extracted from Refs. [12, 25, 39]. We observe that the almost linear behavior, characteristic of irrotational-flow quadrupole dynamics of BM type, is well reproduced by the present approach up to $ L=14 $, with the exception of only the transition strength $ B(E2;16^{+}_{1} \rightarrow 14^{+}_{1}) $ being slighly underestimated. It turns out that the fourth-order term $ X_{4} $ in $ H_{res} $ significantly modifies the values of the ground-state quadrupole collectivity at high angular momenta, and thereby, makes the $ B(E2) $ curve less linear, as observed in Fig. 2. For smaller absolute values of parameter c, we obtain more linear-like behavior. This reproduces the experimental yrast $ B(E2) $ values in $ ^{102} $Pd in a better manner, but, it destroys the strong γ-unstable structure of the γ band. It is important to highlight the significant underestimation of ground-state (yrast) band quadrupole collectivity within the IBM, characterized by a pronounced cut-off effect in the curve. This behavior is typical for transition probabilities calculated using compact spectrum-generating algebra (see, e.g., the discussion concerning Fig. 1 of [10]). Furthermore, similar cut-off behavior was also obtained for $ ^{110} $Cd in Ref. [10] when the rigid-flow quadrupole dynamics was considered. Additionally, in Table 2, we compare the known experimental $ B(E2) $ values [23, 47] with the theory for the nonyrast states of γ and β bands in $ ^{102} $Pd. Among the seven observed $ B(E2) $ transition probabilities, six were found in qualitative agreement. For the quadrupole moment of excited $ 2^{+}_{1} $ state, we obtain $ Q(2^{+}_{1}) = -0.52 eb $ to compare with the experimental value $ -0.20(15) eb $ [48]. We stress that no effective charge is used in our calculations, i.e. $ e=1 $. From Table 2, a disagreement of the transition probability from the $ 0^{+}_{2} $ state of the β band to $ 2^{+} $ state of the γ band is evident, which suggests that probably some important components are missed in the model interaction.

Figure 2.  (color online) Comparison of the experimental [12] and theoretical intraband $ B(E2) $ values in Weisskopf units between the states of the ground band in $ ^{102} $Pd. Theoretical predictions of the five-dimensional collective Hamiltonian based on the relativistic self-consistent mean field without (5DCH) and with (5DCH*) spin-dependent moment of inertia [39], the interacting boson model (IBM) [25], the general collective model (GCM) [25], and the cranking + shell-correction tilted-axis cranking (WS-SCTAC) [12] semiclassical calculations are provided as well. No effective charge is used in the cases of PNSM, WS-SCTAC, 5DCH, and 5DCH*.

i	f	$ B(E2;L_{i}\rightarrow L_{f})_{th} $	$ B(E2;L_{i}\rightarrow L_{f})_{\exp } $
$ 2_{2} $	$ 0_{1} $	$ \ \ \ \ \ \ \ 9.7 $	$ \ \ \ \ \ 2(1) $
$ 2_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ 26.2 $	$ \ \ \ \ \ 15(2) $
$ 2_{2} $	$ 4_{1} $	$ \ \ \ \ \ \ \ 7.1 $	$ \ \ \ \ \ - $
$ 3_{1} $	$ 2_{1} $	$ \ \ \ \ \ \ \ 5.3 $	$ \ \ \ \ \ - $
$ 3_{1} $	$ 4_{1} $	$ \ \ \ \ \ \ \ 4.3 $	$ \ \ \ \ \ - $
$ 3_{1} $	$ 2_{2} $	$ \ \ \ \ \ \ \ 47.6 $	$ \ \ \ \ \ - $
$ 4_{2} $	$ 4_{1} $	$ \ \ \ \ \ \ \ 16.9 $	$ \ \ \ \ \ <8 $
$ 4_{2} $	$ 2_{2} $	$ \ \ \ \ \ \ \ 34.2 $	$ \ \ \ \ \ 45(9) $
$ 4_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ \ 20.3 $	$ \ \ \ \ \ 3(1) $
$ 0_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ \ 0.02 $	$ \ \ \ \ <0.0004 $
$ 0_{2} $	$ 2_{2} $	$ \ \ \ \ \ \ \ \ 0.003 $	$ \ \ \ \ \ 96(40) $

Table 2.  Comparison of the theoretical interband or intraband $ B(E2) $ transition probabilities (in Weisskopf units) for the lowest states of γ and β bands in $ ^{102} $Pd with the known experimental data [23, 25, 47]. No effective charge is used in the calculation.

In Fig. 3 we provide the $S U(3)$ decomposition of the wave functions for the collective states of ground, γ, and β bands in $ ^{102} $Pd for different angular momentum values. In the present scheme, we use the orthonormal Vergados basis [49], labeled as q, obtained by Gram-Schmidt orthogonalization of the Elliott states [29]. Hence, the Vergados basis preserves the physical significance of the Elliott state-labeling prescription to the greatest extent. For example, the Vergados β band, designated as $ q=0 $, is defined as pure Elliott $ K=0 $ band. Vergados γ band, $ q=2 $, consists of Elliott $ K=2 $ and $ K=0 $ states so as to be orthogonal to $ q=0 $. Similarly, the other q bands can be considered in the Vergados basis. Practically, to a given K band in the Elliott basis corresponds a $ q\simeq K $ band in the Vergados basis up to small K-admixtures due to the Elliott-Vergados transformation, which are negligible for comparatively large-dimensional $S U(3)$ irreducible representations or/and small angular momenta (the case of the experimentally observed β and γ bands).

Figure 3.  (color online) $S U(3)$ decomposition of the wave functions for the states of the ground, γ, and β bands in $ ^{102} $Pd for different angular momentum values. The used quantum numbers are $ (\lambda,\mu)q $.

In Fig. 3, it can be observed that $S U(3)$ symmetry is poorly broken and significant K-admixtures are obtained for the states of ground, γ, and β bands, generated by the $ X^{a}_{3} $ and $ X^{a}_{4} $ terms. The observed bands of collective states can still be labeled by the dominant $ q \simeq K $ character. Furthermore, it can be observed that the $ S U(3) $ decomposition amplitudes are spin-dependent, i.e., $S U(3)$ is not a good quasi-dynamical symmetry in the sense provided in Refs. [50, 51]. The latter implies that there is no adiabatic decoupling of the rotational and high-energy vibrational degrees of freedom within the PNSM for $ ^{102} $Pd. These are expected results for vibrational- and transitional-like nuclei with a characteristic energy ratio between that of HV ($ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2 $-$ 2.2 $) and γ-unstable WJ ($ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2.5 $) limits of the BM model. For such nuclei, an important role in nuclear dynamics is played by the coupling of different degrees of freedom. This is also confirmed by the present shell-model calculations for $ ^{102} $Pd. In this regard, it is worth mentioning that the coupling of the collective and quasiparticle excitations, when the adiabatic approximation is not valid, can be considered, e.g., for vibrational and transitional nuclei within the semiclassical tidal-wave approach [13]. The latter is in contrast to the present PNSM application, where the coupling of different collective (irrotational-flow rotational and high-energy vibrational) degrees of freedom is obtained. Generally, the quasiparticle excitations could also be considered in the present symplectic based proton-neutron shell-model approach by including the excited $ S p(12,R) $ irreducible representations. The latter, however, requires an extension of the PNSM computational technique for performing symplectic representation-mixed shell-model calculations by involving different types of symplectic-breaking interactions.

Different staggering functions are widely used to characterize the collectivity in atomic nuclei. For instance, different experimental and theoretical patterns for the quantity [52]

corresponding to various types of collectivity, have been provided in Ref. [53]. The staggering function $ S(L) $ between the states of the γ band is well known to distinguish the type of rotational dynamics. Thus, a small, positive, and constant value of $ +0.33 $, which is a characteristic feature of $ S(L) $ for the axially- symmetric rotor, is obtained. For γ-rigid and γ-unstable quadrupole motion, the staggering patterns show strong odd-even staggering, having minima at odd and even values of L, respectively. We apply function $ S(L) $ provided by (42) to the γ band energies in $ ^{102} $Pd and compare its experimental and theoretical values in Fig. 4. In the figure, it can be observed that the staggering function $ S(L) $ is well described with minima at even L values $ - $ in accordance with the γ-unstable rotor behavior [53]. It is important to note that the type of odd-even staggering between the collective states of the γ band itself can not be used to distinguish between the rigid-flow and irrotational-flow dynamics, because, as demonstrated in the present study, the modified $ X^{a}_{3} $ or/and $ X^{a}_{4} $ terms are able to produce γ-unstable type of staggering $ - $ in contrast to the previous calculations with spin-independent strengths. Moreover, within the present proton-neutron shell-model approach, this type of a γ-unstable staggering can be obtained in both cases when the excitation operator belongs to $S U(3)$ or $S L(6,R)$ algebra generators, i.e., when we have rigid-flow or irrotational-flow type quadrupole dynamics. Thus, a more reliable criterion for distinguishing between the two types of rotational dynamics is the form of the excitation operator and its (classical) dynamical content. Compared to the energy spectra of $ ^{102} $Pd provided in Refs. [23, 25], here the possible $ 6^{+} $ state of the γ band with energy of 3.003 MeV (which is below the $ 5^{+} $ state with energy 3.074 MeV) is included into the calculation.

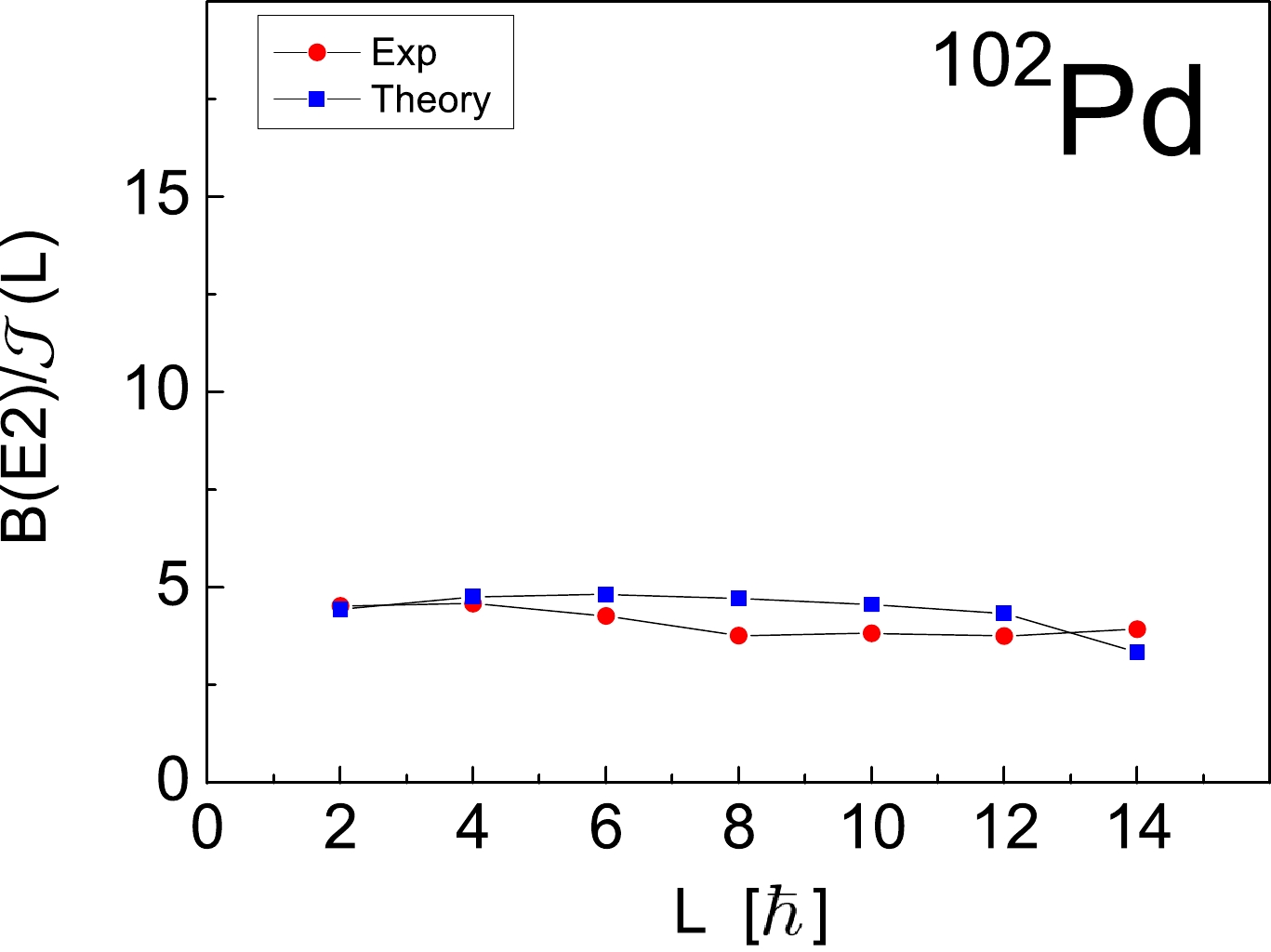
The tidal wave, considered in Refs. [12, 13], was characterized by the following three features: 1) linear increase in $ E(L) $; 2) monotonic linear increase of the yrast $ B(E2) $ values as a function of the angular momentum L; and 3) nearly constant ratio $ B(E2)/\mathcal{J} (L) $. From Figs. 1 and 2 , it can be observed that the first two characteristic features of the tidal wave are satisfied. To test the third characteristic, in Fig. 5, we compare the theoretical value for the (kinematical) moment of inertia for $ ^{102} $Pd, defined by the expression [12]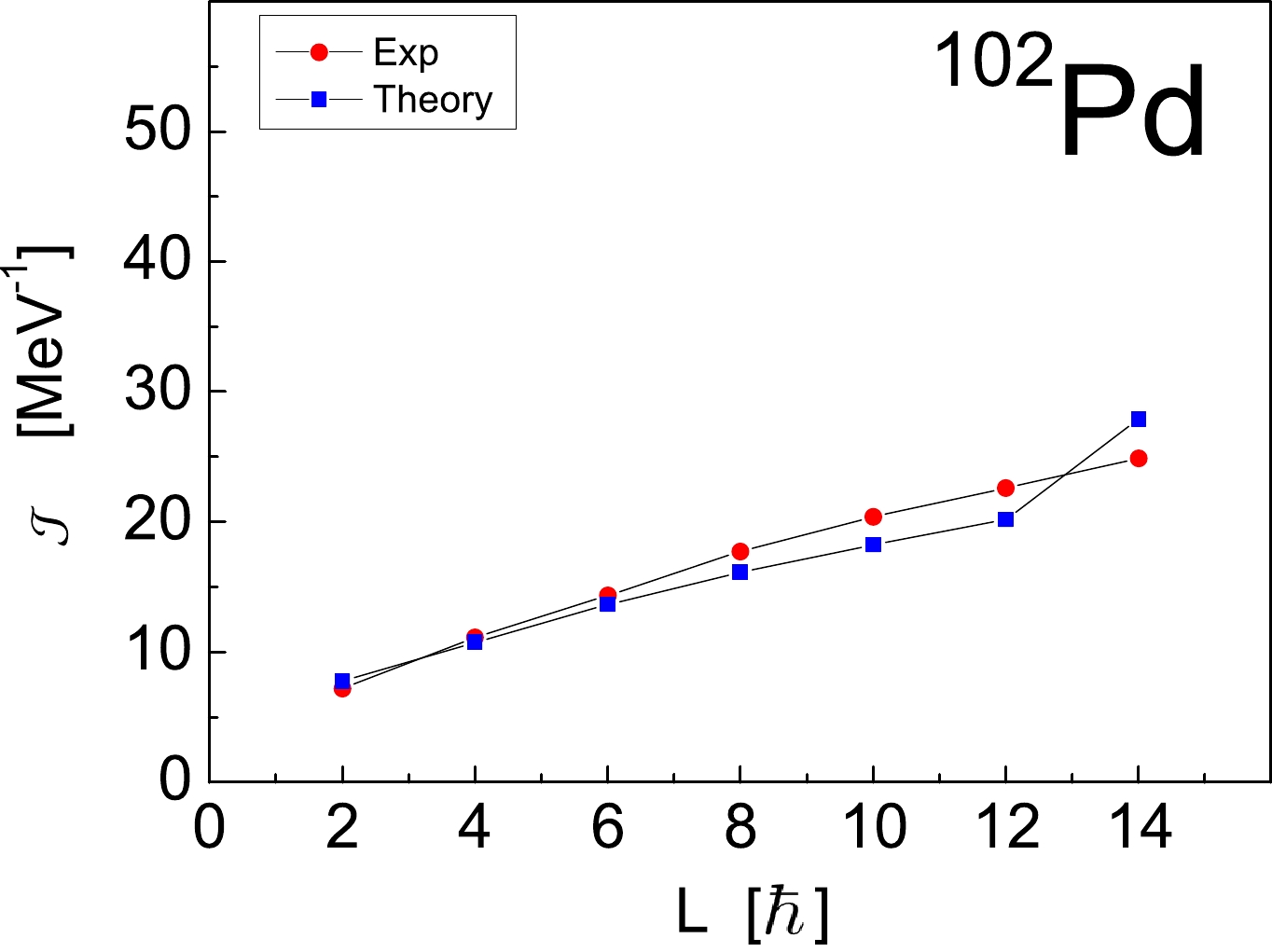

Figure 5.  (color online) Comparison of the experimental and theoretical (kinematical) moment of inertia $ \mathcal{J}(L) $ as a function of the angular momentum L for the yrast band in $ ^{102} $Pd.

with the corresponding experimental values. The figure shows that the experimental moment of inertia for the yrast band is reasonably well described, being slightly underestimated for $ L=8 - 12 $ and slightly overestimated for $ L=14 $. Furthermore, in Fig. 6, we present the theoretical and experimental values for the ratio $ B(E2)/\mathcal{J} (L) $ for the yrast band in $ ^{102} $Pd. From the figure, a nearly constant ratio $ B(E2)/\mathcal{J} (L) $ can be observed for the states of the yrast band. In this way, the present shell-model calculations fulfill all three characteristic properties proposed in Ref. [12], and thereby, support the semiclassical interpretation of "tidal wave" motion suggested for $ ^{102} $Pd. The tidal wave concept [12, 13] provides a new mechanism for the generation of the angular momentum. In contrast to the standard rigid-rotor model, in which the energy and angular momentum increase with the rotational angular frequency, the energy and the angular momentum of the tidal wave increase due to the increase in the deformation (and hence the moment of inertia) while the rotational frequency remains almost constant [12, 13].

Figure 6.  (color online) Comparison of the experimental and theoretical ratio $ B(E2)/\mathcal{J}(L) $ as a function of the angular momentum L for the yrast band in $ ^{102} $Pd.

The structure of the low-lying collective excitations in $ ^{102} $Pd is examined within the recently proposed microscopic shell-model version of the BM collective model. In this regard, we remind that the original BM model for even-even nuclei admits only one shell-model irreducible representation$ - $namely the scalar representation. This representation only produces an irrotational-flow dynamics of BM type. The scalar irreducible representation of the BM model corresponds to the case of doubly closed shell nuclei. In contrast, its microscopic version contains many shell-model representations, which are determined by the underlying fermion structure of the nucleus and are provided by the intrinsic $S p(12,R)$ bandhead structure $ \langle \sigma\rangle $.

The nucleus $ ^{102} $Pd was proposed in the literature as a good example, exhibiting "tidal wave" running on the nuclear surface [12], which corresponds to the original irrotational-flow type quadrupole dynamics of BM type. The microscopic shell-model basis underlying the irrotational-flow collectivity was recently provided in Ref. [10], in which the components of the excitation operator coincide with the infinitesimal generators of irrotational-flow rotation. It has been demonstrated that the irrotational-flow dynamics in the harmonic vibrator and WJ type submodels of the microscopic version of the BM model can be appropriately associated with the Lie algebra of $S L(6,R) -$ the group of volume preserving deformations and rotations in the six-dimensional collective space $ \mathbb{R}^{6} $, spanned by the microscopic proton-neutron quadrupole-monopole operators $ Q_{ij}(p,n) $. To reveal the dynamical content of the PNSM and its physics, we reconsidered in more detail the physical significance of the symplectic generators, generating the basic collective flows in the many-particle proton-neutron nuclear system. In this way, the nature of low-energy quadrupole states can directly be related to the form of the excitation quadrupole operator (e.g., $S U(3)$ or $S L(6,R)$ [10]), following directly from the physical significance of the algebraic operators generating rigid or irrotational dynamical flows.

To calculate the low-energy spectrum of $ ^{102} $Pd, we used a dynamical symmetry Hamiltonian, which is expressed along the reduction chain defining the microscopic shell-model version of the BM model, and a residual rotor part and vertical mixing term that mixes different $ S U(3) $ and $ S O(6) $ multiplets within the relevant $ S p(12,R) $ irreducible collective space $0p-0h\; [24]_{6}$ of $ ^{102} $Pd. We performed a simultaneous diagonalization of the model Hamiltonian within the space of different $ S U(3) $ and $ S O(6) $ irreps that belong to the $ S L(6,R) $ irrep $ \upsilon_{0}=24 $ from one side, and in the space of different $ q \simeq K $ values within each $ S U(3) $ multiplet from another side. The relevant $ S p(12,R) $ and $S L(6,R)$ irreducible shell-model representations have been determined using the proxy-$ S U(3) $ scheme.

A good description of the excitation energies of the lowest ground, γ, and β bands, including the strong odd-even staggering pattern between the collective states of the γ band and some other energy-dependent quantities in $ ^{102} $Pd, is obtained. The low-energy intraband and interband quadrupole dynamics, using the $S L(6,R)$ infinitesimal generators of irrotational-flow (surface-wave) rotations as quadrupole excitation operators, is reasonably well described within the present proton-neutron sympletic based shell-model approach without the use of an effective charge. We indicate that the description of the excitation energies and ground-state intraband $ B(E2) $ transition strengths can be improved by including other components of the nuclear interaction $ - $ for instance, the second-order $S O(6)$ and third-order $S U_{pn}(3)$ Casimir operators. The findings of the present study support the semiclassical interpretation of tidal wave introduced some years ago [12, 13] for the description of the yrast band for some vibrational and transitional nuclei and extend its irrotational-flow character to the excited γ and β bands, because the same excitation operator is used. At the same time, in contrast to the semiclassical approach of Refs. [12, 13], the present microscopic shell-model version of the BM model within the framework of the PNSM is pure quantal in nature and can be used to properly describe the observed fermion dynamics in atomic nuclei, exploiting the well-defined many-nucleon quantum mechanics. Thus, the obtained results shed light on the question of the existence and the microscopic shell-model foundation of the irrotational-flow type quadrupole dynamics, which lies on the ground of the original BM model of quantized vibrations and surface-wave rotations in atomic nuclei.