-
Einstein's gravitational theory (GR) serves as a cornerstone that provides a comprehensive description of the gravitational field and matter on cosmic scales. In GR, spacetime is described using mathematical structures defined by the Riemann's metric. This metric encodes information about distances and angles in spacetime and allows physicists to understand the curvature of spacetime caused by gravity. However, Weyl [1] introduced the concept of a length connection, which is different from the standard metric connection used in Riemannian geometry. Weyl's theory focuses on gauging the conformal factor adjusting the scale of distances. Weyl introduced the concept of non-metricity, which assures that divergence of the metric tensor exists. This departure from Riemannian geometry is a new perspective on the geometric nature of spacetime. Non-Riemannian geometries incorporate additional geometric quantities such as torsion and non-metricity. Torsion refers to the twisting or rotation of spacetime, while non-metricity involves deviations from the standard concept of distance allowing for a broader understanding of spacetime geometry. Torsion represents a gravitational interaction with teleparallel gravity instead of GR [2]. The teleparallel equivalent to GR reformulates gravity not as a result of spacetime curvature but rather through torsion. In this framework, the connection used has zero curvature but non-zero torsion and is still metric-compatible, meaning that there is no non-metricity. Symmetric teleparallel gravity provides a different perspective on gravity, focusing on non-metricity as the source of gravitational effects in a flat spacetime scenario, that is, zero curvature and zero torsion [3]. Various extended theories of gravity in different contexts have been discussed in [4−14].
Xu et al. [15] introduced the
$ f({Q},{T}) $ theory by including the trace of the energy-momentum tensor in the action of symmetric teleparalell theory. This proposal comprises theoretical implications, compatibility, and relevance in cosmology. In recent research, various studies have delved into the implications of modified$ f({Q},{T}) $ gravity. Fajardo [16] emphasized that this modified theory offers alternatives to the standard cosmological model. Arora et al. [17] conducted a study where they constrained several free parameters in two distinct$ f({Q},{T}) $ models through various energy conditions. Their analysis shed light on the viability of this theory, paving a way for a new approach to understand the dark sector of the universe. Tayde et al. [18, 19] explored the feasibility of traversable wormholes through strange matter in an$ f({Q},{T}) $ background. Pradhan et al. [20] discussed various physical characteristics of gravastars such as proper length, energy, entropy, and surface energy density in this framework and found a stable gravastar model. Bourakadi et al. [21] conducted a comprehensive study on the black holes in this gravity. Loo et al. [22] investigated the$ f({Q},{T}) $ theory with small anisotropy to study the complete cosmic evolution as our universe is not isotropic since the Planck era. Narawade et al. [23] studied the cosmic accelerated expansion in an extended symmetric teleparallel gravity to understand the evolutionary phase of the universe in the modified theory. Khurana et al. [24] stated that this modified theory presents valuable insights into the late time cosmic acceleration. Shukla et al. [25] investigated an isotropic and homogeneous universe model in this framework by examining a deceleration parameter.Viable characteristics of stellar objects endorse significant progress in alternative theories. Ilyas and Ahmad [26] used observational data from various CS candidates to investigate the behavior of static spherical structures in the framework of
$f(R)$ gravity. Rej and Bhar [27] employed the Durgapal-IV metric to analyze the physical characteristics of anisotropic static spherical solutions in$f(R,T)$ theory. Their examination confirmed that the obtained results remain in the physically acceptable range. Das [28] delved into stable spherically symmetric stellar configurations in$f(R,G)$ gravity. Malik et al. [29] analyzed the charged anisotropic characteristics of CSs using the Karmarkar condition in the modified Ricci-inverse gravity. Ditta and Tiecheng [30] discussed a comprehensive analysis of the physical properties of CSs in Rastall teleparallel gravity. Sharif and Gul [31] verified the stability of proposed CSs using sound speed method in squared gravity.Nashed and Capozziello [32] investigated the viable model for neutron stars in
$f(R)$ gravity, suggesting intriguing possibilities to understand the gravitational behavior of dense objects. Dey et al. [33] explored the viable anisotropic stellar objects employing the Finch-Skea solutions in the$f(R,T)$ framework. Rej et al. [34] conducted a detailed examination of the charged CSs in the same theoretical framework, unveiling valuable insights into the interplay between charge and gravity in compact stellar systems. Kumar et al. [35] investigated crucial insights into the relationship between$f(R,T)$ gravitational theory and the internal dynamics of CSs. Maurya et al. [36] used the Karmarkar condition to probe charged relativistic objects in$f(G,T)$ gravity. Shamir and Malik [37] provided valuable insights into the dynamical stability of compact spherical systems in the modified framework. Lin and Zhai [38] investigated the influence of effective fluid parameters on the geometry of CSs in the$f(Q,T)$ theory. The geometry of compact stars with different considerations in$f(Q)$ and$f(Q,T)$ theory has been studied in [39−45].The abovementioned literature emphasizes the importance of exploring the viable attributes of CSs in
$f(Q,T)$ theory. This paper is organized as follows. In Section II, we present the field equations of$f(Q,T)$ gravity and evaluate the unknown parameters through the Darmois junction conditions. Section III examines different physical quantities to identify the physical characteristics exhibited by CSs. Section IV analyzes the equilibrium state and stability of CSs, providing insights into their dynamic behavior. The findings and implications of our results are presented in Section V. -
The main objective of this section is to provide an outline of the process by which the field equations are formulated using the variational principle in the modified
$f(Q,T)$ theory. This modified theory has gained significant attention owing to its potential explanations for various cosmological phenomena. The gravitational action in this framework is altered by the addition of extra terms that are based on non-traditional geometric measures apart from the metric tensor. The motivation behind considering this modified theory lies in the quest for a more comprehensive framework to describe gravity and the cosmic phenomenon.The action of this theory is expressed as [15]
$ {\rm{I}}=\frac{1}{2}\int \bigg[f(Q,T)+2 {L}_{m}\bigg]\sqrt{-g} \,{\rm d}^{\, 4}x, $

(1) where
$ L_m $ is the Lagrangian of matter. The non-metricity and deformation tensor are defined as$ \begin{aligned}[b] Q =\;&-g^{\gamma\eta}({L}^{\lambda}_{\; \xi\gamma} {L}^{\xi}_{\; \lambda\eta} -L^{\lambda}_{\; \xi\lambda}{L}^{\xi}_{\; \gamma\eta}), \\ {L}^{\lambda}_{\; \xi\gamma}=\;&-\frac{1}{2} g^{\lambda\varsigma} (\nabla_{\gamma}g_{\xi\varsigma}+\nabla_{\xi} g_{\varsigma\lambda} -\nabla_{\varsigma}g_{\xi\gamma}).\end{aligned} $

(2) However, the super-potential of this model is as follows:
$ P^{\lambda}_{\; \gamma\eta}=\frac{1}{4}\big[(Q^{\lambda} -\bar{Q}^{\lambda})g_{\gamma\eta}- \delta ^{\lambda} _{\; (\gamma Q_{\eta})}\big]-\frac{1}{2} L^{\lambda}_{\; \gamma\eta}, $

(3) The relation for Q is
$ Q=-Q_{\lambda\gamma\eta} P^{\lambda\gamma\eta}=\frac{1}{4}(Q^{\lambda\eta\xi} Q_{\lambda\eta\xi}-2Q^{\lambda\eta\xi} Q_{\xi\lambda\eta}+2Q^{\xi}\bar{Q}_{\xi}-Q^{\xi} Q_{\xi}), $

(4) where
$ Q_{\lambda\gamma\eta}=\nabla_{\lambda} g_{\gamma\eta} =-\partial g_{\gamma\eta,\lambda}+g_{\eta\xi} \bar{\Gamma}^{\xi}_{\; \gamma\lambda} +g_{\xi\gamma}\bar{\Gamma}^{\xi}_{\; \eta\lambda}. $

The calculation of the above relation (4) and its detailed variation is given in [15]. Varying the action (1) corresponding to
$ g_{\gamma\eta} $ , we have$ \begin{aligned}[b] T_{\gamma \eta} =\;&\frac{-2}{\sqrt{-g}} \nabla_\lambda\left(f_{Q} \sqrt{-g} {P}^\lambda{ }_{\gamma \eta}\right)-\frac{1}{2} f g_{\gamma \eta}+f_{T}\left(T_{\gamma \eta}+\Theta_{\gamma \eta}\right) \\ &-f_{Q}\left(P_{\gamma \lambda \xi} Q_\eta{ }^{\lambda \xi}-2 Q^{\lambda \xi}{ }_\gamma P_{\lambda \xi \eta}\right), \end{aligned} $

(5) where
$f_{T}$ and$f_{Q}$ are the partial derivatives corresponding to T and Q.Consider a static spherical spacetime as the interior region of stellar objects to examine the geometry of CSs, which is defined as
$ {\rm d} s^{2}={\rm d}t^{2}{\rm e}^{\vartheta(r)}-{\rm d}r^{2} {\rm e}^\varpi{(r)}-r^{2}{\rm d}\Omega^{2}, $

(6) where
${\rm d}\Omega^{2}={\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi^{2}$ . The anisotropic matter distribution is given by$ {T}_{\gamma\lambda}= {U}_{\gamma} {U}_{\lambda} \varrho + {V}_{\gamma} {V}_{\lambda} p_{r}-p_{t}g_{\gamma\lambda} + {U}_{\gamma} {U}_{\lambda}p_{t} - {V}_{\gamma} {V}_{\lambda}p_{t}, $

(7) where
${V}_{\gamma}$ is 4-vector and$U_{\gamma}$ is 4-velocity of the fluid. The matter-Lagrangian is important in various cosmic phenomena as it demonstrates the configuration of fluid in spacetime. The particular value of the matter-Lagrangian can yield significant insights. The well known used formulation of the matter-Lagrangian in the literature is$L_{m}=-\dfrac{p_{r}+2p_{t}}{3}$ [46−48]. The modified field equations for the static spherical spacetime become$ \begin{aligned}[b] \varrho = \;&\frac{1}{2r^{2}{\rm e}^{\varpi}}\bigg[2r{Q}'f_{Q} {Q}({\rm e}^{\varpi}-1) +f_{Q}\big(({\rm e}^{\varpi}-1)(2+r\vartheta')\\&+({\rm e}^{\varpi}+1)r\varpi' \big) +fr^{2}{\rm e}^{\varpi}\bigg]-\frac{1}{3}f_{T}(3\varrho+p_{r}+2p_{t}), \end{aligned} $

(8) $ \begin{aligned}[b] p_{r}=\;&\frac{-1}{2r^{2}{\rm e}^{\varpi}}\bigg[2r{Q}'f_{QQ}({\rm e}^{\varpi}-1) +f_{Q}\big(({\rm e}^{\varpi}-1)\\&\times(2+r\vartheta'+r\varpi')-2r\vartheta'\big) +fr^{2}{\rm e}^{\varpi}\bigg]+\frac{2}{3}f_{T}(p_{t}-p_{r}), \end{aligned} $

(9) $ \begin{aligned}[b] p_{t}=\;&\frac{-1}{4r{\rm e}^{\varpi}}\bigg[-2rQ'\vartheta'f_{QQ} +f_{Q}\big(2\vartheta'({\rm e}^{\varpi}-2)-r\vartheta'^{2}\\&+\varpi'(2e^{\varpi}+r\vartheta') -2r\vartheta"\big)+2fr{\rm e}^{\varpi}\bigg]+\frac{1}{3}f_{T} (p_{r}-p_{t}). \end{aligned} $

(10) The field equations are complicated because of multivariate functions and their derivatives. We take a specific model as [49]
$ f(Q,T)=\alpha Q+\beta T, $

(11) where α and β are model parameters. This model enhances our ability to explain gravitational interactions and their connection with matter and energy. This model provides more accurate predictions for mysterious components of the universe phenomena by refining of mathematical framework and introducing new dynamical mechanisms. Furthermore, this model stands as a pivotal pursuit in theoretical physics as it aims to unravel the fundamental essence of physical phenomena from the smallest to the largest scales. It emerges from the aspiration for a unified framework capable of elegantly encompassing a wide array of phenomena spanning from cosmology to particle physics. The resulting field equations become
$ \begin{aligned}[b] \varrho=\;&\frac{\alpha {\rm e}^{-\varpi}}{12r^2(2\alpha^{2}+\beta-1)}\bigg[ \beta(2r(-\varpi'(r \vartheta'+2)+2r\vartheta"\\&+\vartheta'(r \vartheta'+4))-4{\rm e}^{\varpi} +\;4)+3\beta r(\vartheta'(4-r \varpi'+r \vartheta')\\&+2r\vartheta")+12 (\beta-1)(r \varpi'+{\rm e}^{\varpi}-1)\bigg], \end{aligned} $

(12) $ \begin{aligned}[b] p_{r}=\;&\frac{\alpha {\rm e}^{-\varpi}}{12r^2(2\beta^{2}+\beta-1)}\bigg[ 2\beta\big(r\varpi'(r \vartheta'+2)+2({\rm e}^{\varpi}-1)\\&-r(2r\vartheta"+\vartheta'(r \vartheta' +\;4))\big)+3\big(r\big(\beta \varpi'(r \vartheta'+4)\\&-2\beta r \vartheta"-\vartheta'(-4\beta+\beta r \vartheta'+4)\big)\\&-4(\beta-1) ({\rm e}^{\varpi}-1)\big)\bigg], \end{aligned} $

(13) $ \begin{aligned}[b] p_{t}=\;&\frac{\alpha {\rm e}^{-\varpi}}{12r^2(2\beta^{2}+\beta-1)}\bigg[ 2\beta\big(r\varpi'(r \vartheta'+2)+2({\rm e}^{\varpi}-1)\\&-r(2r\vartheta"+\vartheta' (r \vartheta'+4))\big)+3\big(r \big(2(\beta-1)r \vartheta'' \\ &-((\beta-1)r \vartheta'-2)(\varpi'-\vartheta')\big) +\, 4\beta({\rm e}^{\varpi}-1)\big)\bigg]. \end{aligned} $

(14) Here, the metric functions (ϑ, ϖ) must be finite and non-singular to obtain the singular free spacetime. In this regard, we consider the Finch Skea solutions, which are considered as a significant tool to find the exact viable solutions for interior spacetime, defined as [50]
$ {\rm e}^{\vartheta(r)}=(x+\frac{1}{2}yr\sqrt{zr^{2}})^{2},\quad {\rm e}^{\varpi(r)}=1+zr^{2}, $

(15) The arbitrary constants are denoted by x, y, and z, respectively. We can evaluate the values of unknown constants by the Darmois junction conditions. Further, we consider a spherically symmetric vacuum solution as the exterior spacetime. The exterior spacetime is given by
$ {\rm d} s^{2}_+= {\rm d} t^{2}\aleph- {\rm d} r^{2}\aleph^{-1}-r^{2}{\rm d}\Omega^{2}, $

(16) where
$ \aleph=\left(1-\dfrac{2m}{r}\right) $ . The continuity of metric coefficients at the surface boundary$ (r=\mathcal{R}) $ gives$ \begin{aligned}[b] g_{tt}=\;& \left(x+\frac{1}{2}y\mathcal{R}\sqrt{z\mathcal{R}^{2}}\right)^{2}=\aleph, \\ g_{rr}=\;&1+z\mathcal{R}^{2}=\aleph^{-1}, \\ g_{tt,r}=\;&y\mathcal{R}\sqrt{z}\left(x+\frac{1}{2} y\mathcal{R}\sqrt{z\mathcal{R}^{2}}\right)=\frac{m}{\mathcal{R}^{2}}. \end{aligned} $

The solution of these equations gives
$ x=\frac{2\mathcal{R}-5m}{2\sqrt{\mathcal{R}^{2}-2m\mathcal{R}}}, \quad y=\frac{1}{\mathcal{R}}\sqrt{\frac{m}{2\mathcal{R}}}, \quad z=\frac{2m}{\mathcal{R}^{2}(\mathcal{R}-2m)}. $

These constants are important to comprehend the interior of CSs. The mass and radius values for the considered stellar objects are presented in Table 1, and the associated constants can be found in Table 2. In the analysis of stellar objects, it is essential to examine the behavior of metric elements to ascertain the smoothness and absence of singularities in the spacetime. The graphical representation depicted in Fig. 1 serves as a crucial tool in this evaluation process. It is clear that both metric components display consistent patterns and show an increasing trend. This behavior is significant as it indicates the absence of any abrupt or irregular fluctuations in the spacetime metrics associated with the stellar objects under consideration. Thus, based on the graphical analysis presented in Fig. 1, we can assert that the spacetime appears to be smooth and devoid of singularities, meeting the required criteria for our investigation.
CSs $ m_{\odot} $ 

$\mathcal{R}/\rm km$ 

Her X - 1 [51] 0.85 $ \pm $ 0.15

8.1 $ \pm $ 0.41

EXO 1785-248 [52] 1.30 $ \pm $ 0.2

10.10 $ \pm $ 0.44

SAX J1808.4-3658 [53] 0.9 $ \pm $ 0.3

7.951 $ \pm $ 1.0

4U 1820-30 [54] 1.58 $ \pm $ 0.06

9.1 $ \pm $ 0.4

Cen X-3 [55] 1.49 $ \pm $ 0.08

9.178 $ \pm $ 0.13

SMC X-4 [51] 1.29 $ \pm $ 0.05

8.831 $ \pm $ 0.09

PSR J1903+327 [56] 1.667 $ \pm $ 0.021

9.48 $ \pm $ 0.03

LMC X-4 [55] 1.04 $ \pm $ 0.09

8.301 $ \pm $ 0.2

Table 1. Values corresponding to input parameters.
CSs x y z Her X - 1 −0.924111 0.0343333 0.00682713 EXO 1785-248 −0.908173 0.0304946 0.00599414 SAX J1808.4-3658 −0.918476 0.0363264 0.00792193 4U 1820-30 −0.881827 0.0393097 0.0126622 Cen X-3 −0.887784 0.0376881 0.0108966 SMC X-4 −0.89724 0.0371547 0.00969829 PSR J1903+327 −0.880727 0.0379742 0.0119768 LMC X-4 −0.910411 0.0366062 0.00849917 Table 2. Values of unknown parameters.
-
In this section, we examine the viable features of CSs using graphical analysis. For viable and stable CSs with a specific radius, the following conditions need to be satisfied:
● The metric coefficients need to be monotonically increasing and non-singular at the center, which ensures that the spacetimes do not contain any type of irregularities.
● The behavior of matter contents should be monotonically decreasing and
$ p_{r}(r=\mathcal{R})=0 $ to assure that the CSs have a stable denser core.● The matter gradient must vanish at the core and then demonstrate negative behavior toward the boundary.
● Positive energy bounds ensure the presence of normal matter in the stellar objects, which is necessary for a viable geometry of CSs.
● The EoS parameters must fall in the range of [0, 1] for stellar structures to be viable.
● The mass function must be continuous at the core and then show a positively increasing behavior.
● The compactness and redshift functions must be less than
$ \dfrac{4}{9} $ and 5.21, respectively, for a viable geometry of CSs.● The forces must satisfy the equilibrium condition to maintain stability.
● For CSs to be stable, the velocities of sound speed should remain in the range of [0, 1], whereas the adiabatic index must be greater than 1.33.
These constraints provide a framework to understand the behavior of CSs and ensure that their properties are consistent.
-
The investigation of fluid parameters such as density and pressure is essential to understand the internal features of neutron stars. These matter variables are anticipated to be maximum at the core due to their intense density, counteracting gravitational forces and maintaining the stability of CSs against collapse. The corresponding field equations are as follows:
$ \begin{aligned}[b] \varrho=\;&\alpha\bigg[-3yzr^{3}(3+zr^{2})+2yr(15+zr^{2}(13+zr^{2}))\beta\\&+2x(3+zr^{2})\sqrt{zr^{2}} s(2\beta-3)\bigg]\bigg[3(1+zr^{2})^2(yzr^{3}\\&+2x\sqrt{zr^{2}})(\beta-1+2\beta^{2})\bigg]^{-1}, \end{aligned} $

(17) $ \begin{aligned}[b] p_{r}=\;&\alpha z \bigg[2x\sqrt{zr^{2}}(3+zr^{2}(2\beta-3)+6\beta)\\&-yr(6(2+\beta)+zr^{2}(9-10\beta+z r^{2}(2\beta-3)))\bigg]\\&\times\bigg[3(1+zr^{2})^2(yzr^{3}+2x\sqrt{zr^{2}})(\beta-1+2\beta^{2})\bigg]^{-1}, \end{aligned} $

(18) $ \begin{aligned}[b] p_{t}=\;&\alpha z \bigg[2x\sqrt{zr^{2}}(3+(6+4zr^{2})\beta)+yr(-6(2+\beta)\\&+zr^{2}(-3+(4zr^{2}-2) \beta))\bigg]\bigg[3(1+zr^{2})^2(yzr^{3}\\&+2x\sqrt{zr^{2}})(\beta-1+2\beta^{2})\bigg]^{-1}. \end{aligned} $

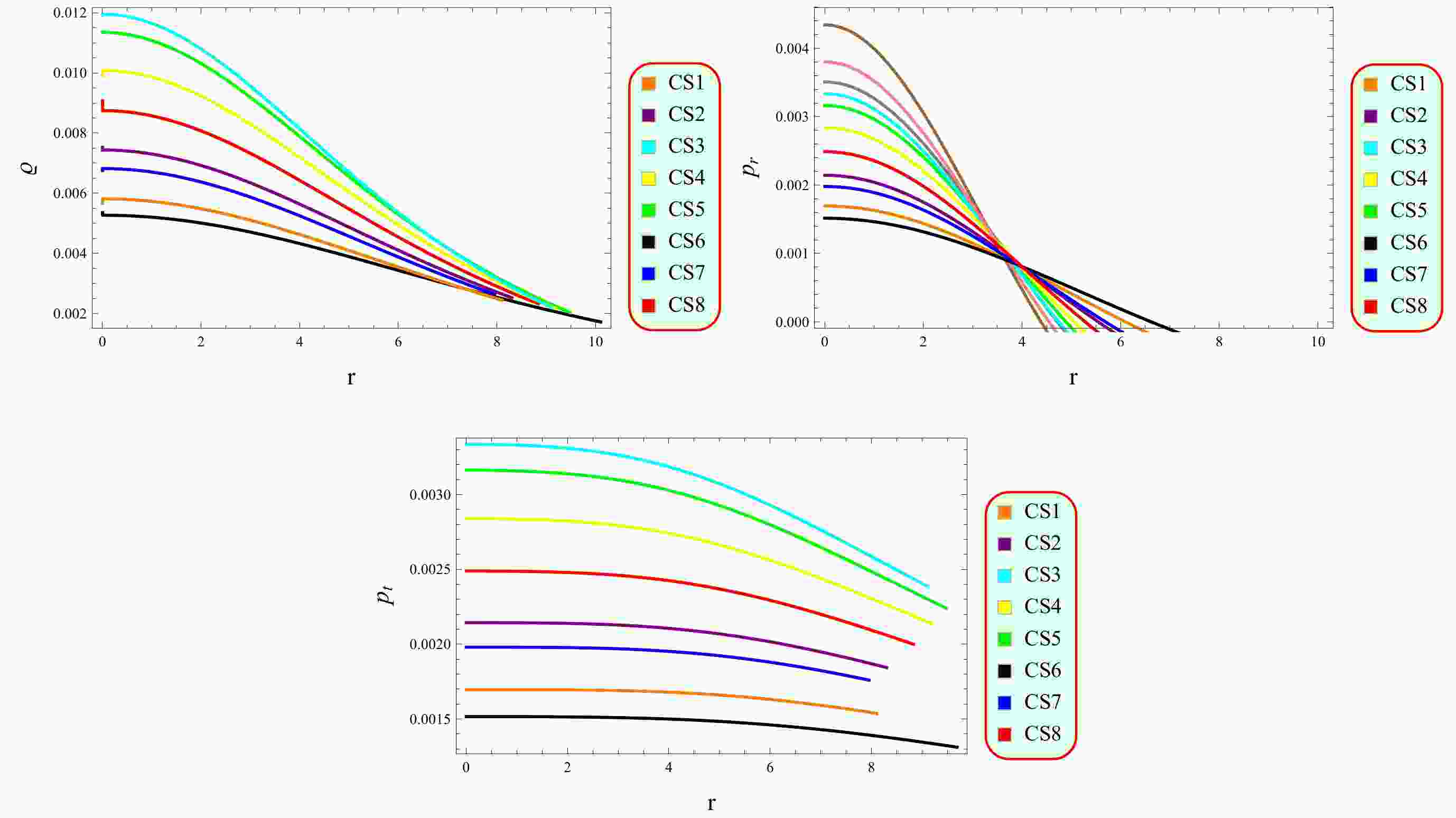
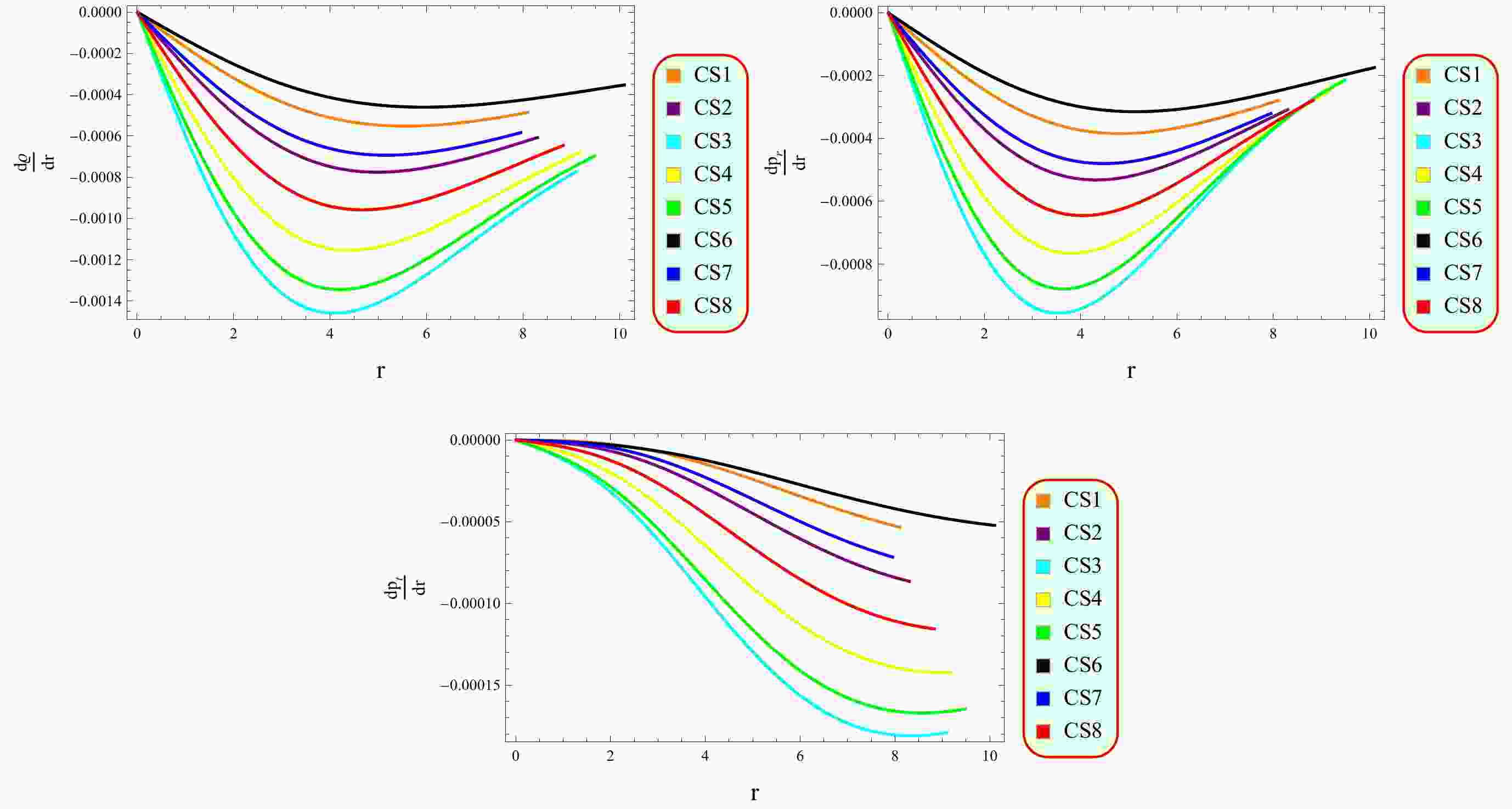
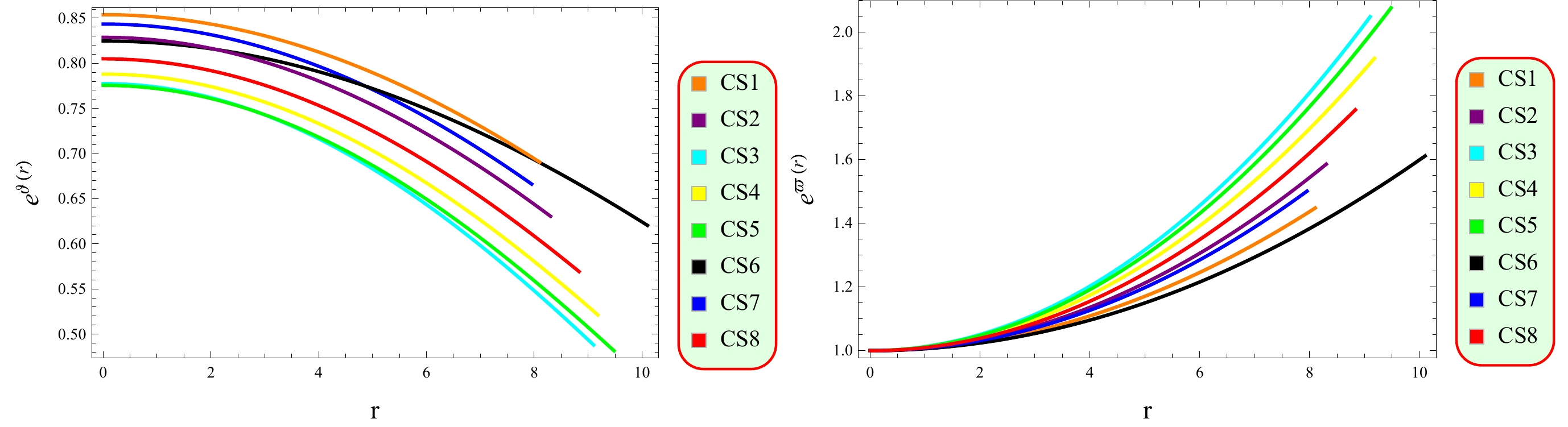
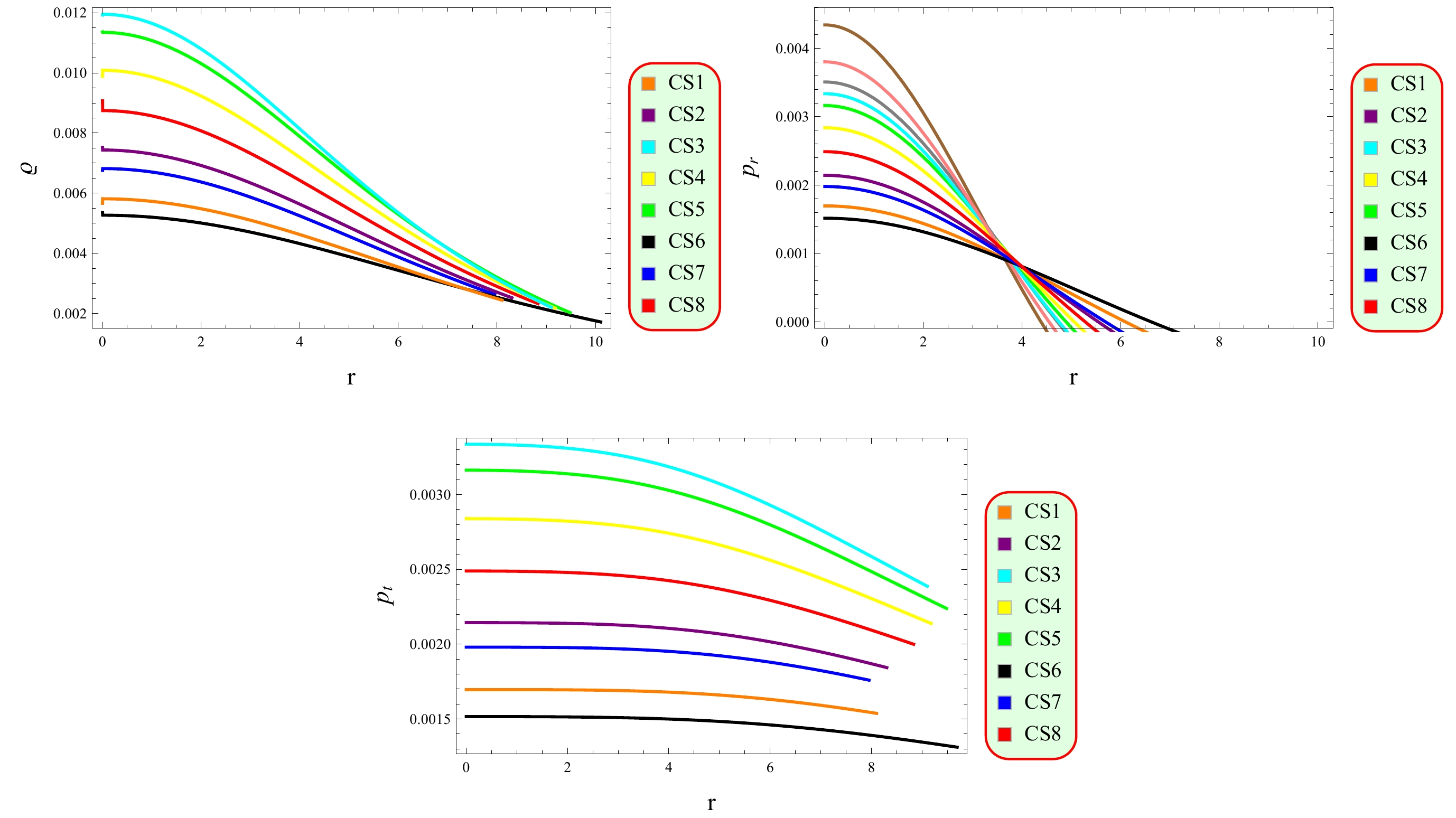
(19) The plots in Fig. 2 indicate that the matter contents are maximum at the core before decreasing, highlighting the dense nature of CSs. Additionally, the radial pressure in the considered CSs shows a consistent decrease as distance from the center increases, until it dissipates at the boundary. Figure 3 shows that CSs have highly dense structures in this framework as the gradient of density and pressure components vanish at the core and become negative thereafter.
-
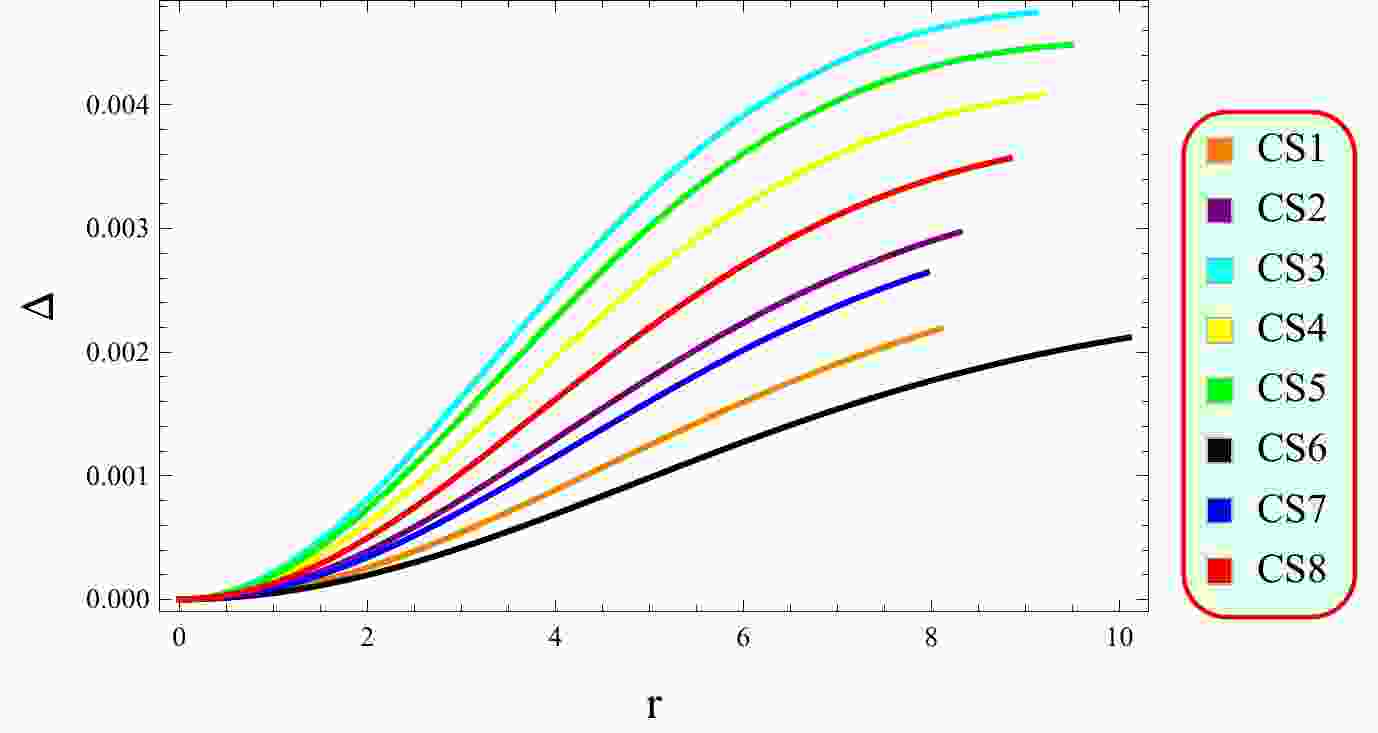
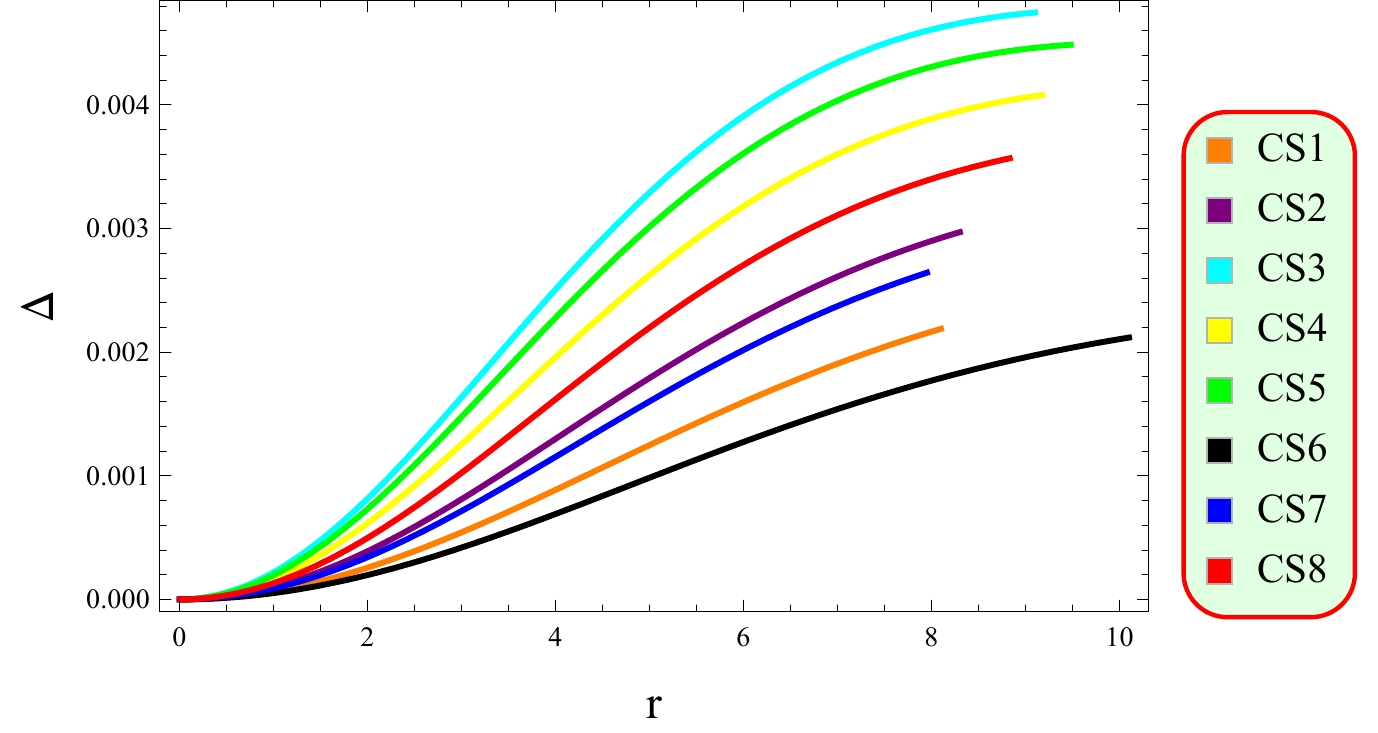
An anisotropic fluid refers to a fluid that exhibits different physical properties or behavior in different directions. The term "anisotropic" comes from the Greek words "aniso" meaning unequal or different and "tropos" meaning direction. Anisotropy refers to a difference in pressure along different directions in the system. The pressure in a star is isotropic when no additional forces or anisotropic effects are present. However, in certain situations such as the presence of strong magnetic fields or other factors, pressure becomes anisotropic. One example of anisotropy is the gravitational field around a rotating object. The gravitational field surrounded by rotating massive objects such as a spinning black hole is not uniform in all directions. The gravitational attraction is stronger in some directions than in others, resulting in anisotropic effects. This phenomenon is known as frame-dragging, where the rotation of the object drags the surrounding spacetime along with it. Figure 4 indicates the existence of a repulsive force as the behavior of anisotropy is positive, which plays a crucial role in sustaining large-scale structures and preventing gravitational collapse.
-
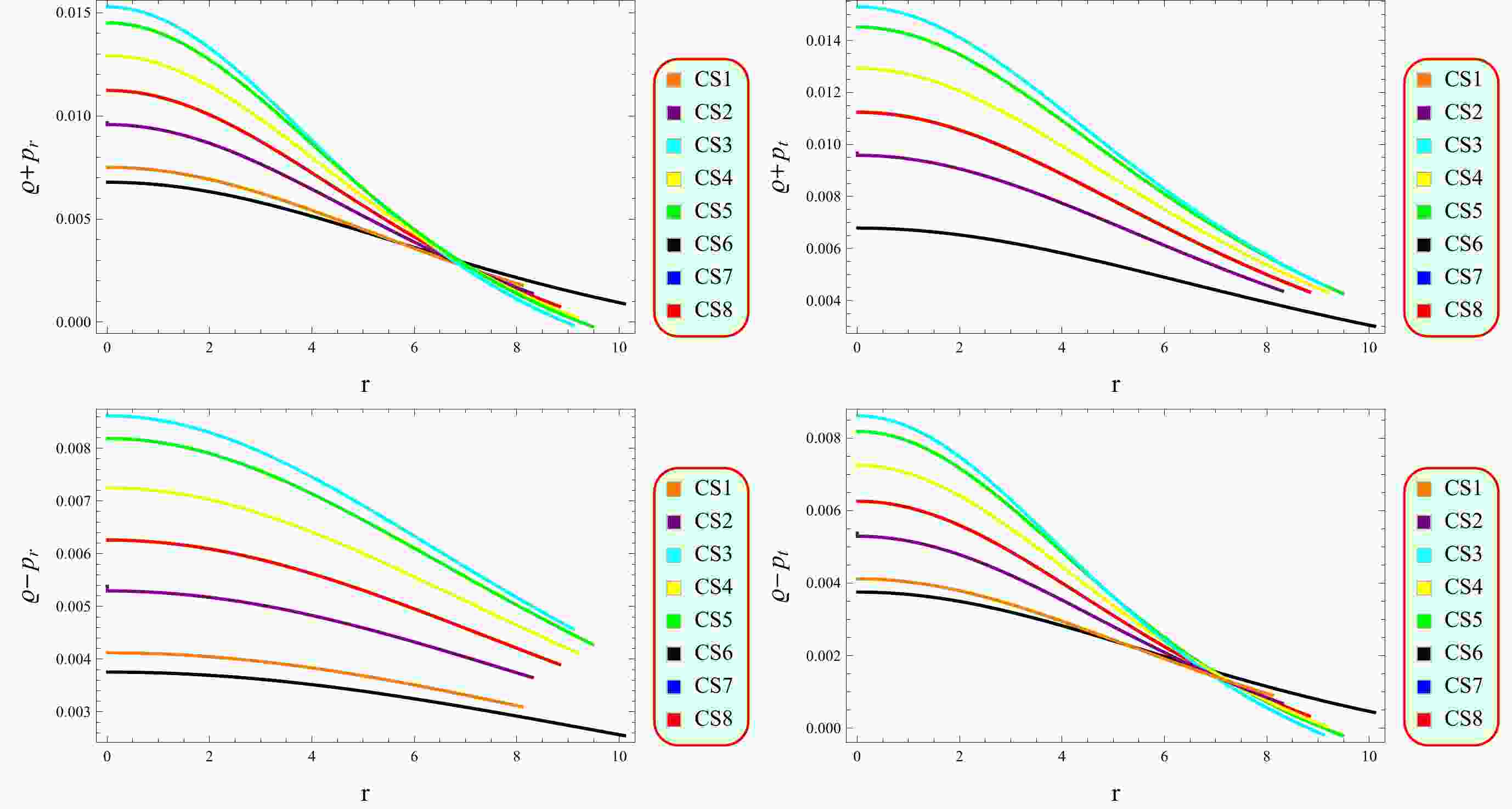
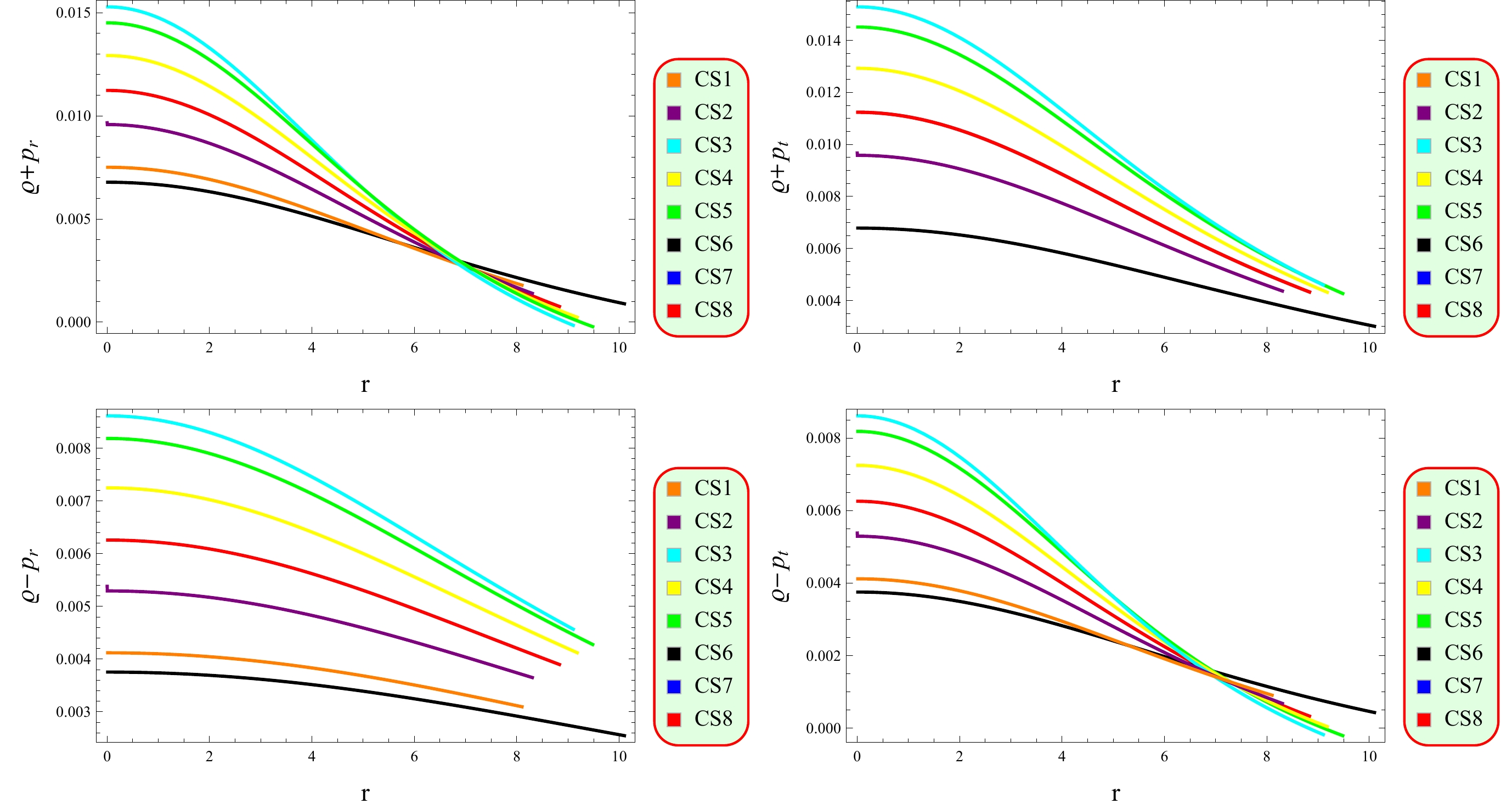
Astrophysical entities are composed of a variety of materials in their composition and it is important to differentiate the types of matter (exotic/ordinary) present in the celestial objects. Energy constraints are necessary to examine the viable fluid configurations in the system. These limitations play a crucial role in investigating the presence of specific cosmic formations and understanding how matter and energy interact under the influence of gravity. These constraints manifest the physical viability of the matter configuration in the neutron stars. The energy conditions are characterized into four types:
● Null Energy Condition
$ 0\leq \varrho+p_{r} , \quad 0\leq \varrho+p_{t}. $

● Dominant Energy Condition
$ 0\leq \varrho\pm p_{r}\geq 0 , \quad 0\leq \varrho\pm p_{t}. $

● Weak Energy Condition
$ 0\leq \varrho+p_{r}+\geq 0 ,\quad 0\leq \varrho+p_{t} , \quad 0\leq \varrho. $

● Strong Energy Condition
$ 0\leq \varrho+p_{r} , \quad 0\leq \varrho+p_{t} , \quad 0\leq \varrho+p_{r}+2p_{t}. $

Scientists can gain insights into the nature and behavior of cosmic structures by analyzing these energy bounds and their effects on the stress-energy tensor, thus contributing to our understanding of the dynamics and evolution of the universe. Figure 5 shows that the considered CSs are viable as all energy constraints are satisfied in the presence of modified terms.
-
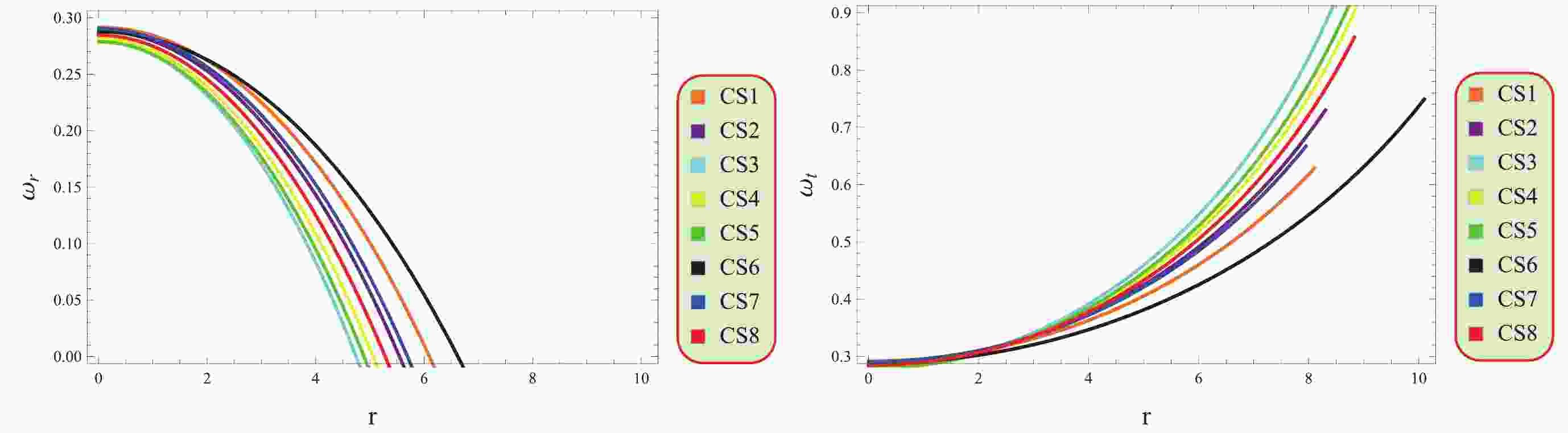
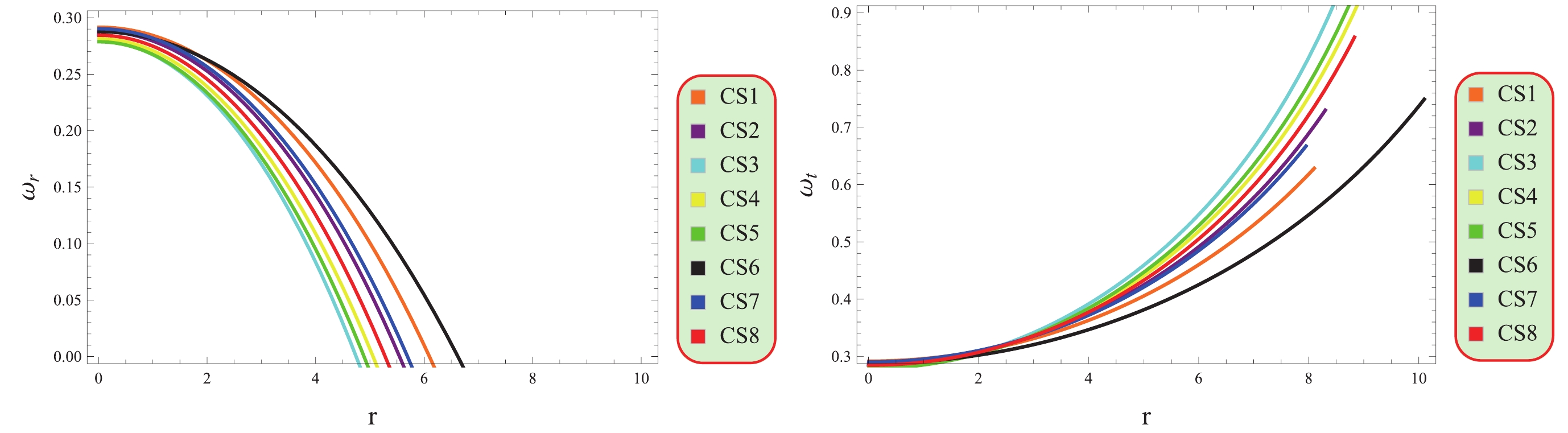
The EoS parameters explain how energy density is related to anisotropic pressure in different types of systems. The radial component
$\Big(\omega_{r}=\dfrac{p_{r}}{\varrho}\Big)$ and transverse component$\Big(\omega_{t}=\dfrac{p_{t}}{\varrho}\Big)$ of EoS parameters must satisfy the range [0, 1] for viable stellar stars [57]. Using Eqs. (17)−(19), we have$ \begin{aligned}[b] \omega_{r}=\;&\bigg[2x\sqrt{zr^{2}}(3+zr^{2}(3-2\beta)+6\beta)-yr(6(2+\beta)\\&+zr^{2}(9-10\beta +zr^{2}(2\beta-3)))\bigg]\bigg[2x\sqrt{zr^{2}}(3+zr^2)(2\beta-3)\\&+y(30r\beta+z^{2}r^{5} (2\beta-3)+zr^{3}(26\beta-9))\bigg]^{-1},\\ \omega_{t}=\;&\bigg[2x\sqrt{zr^{2}}(3+(6+4zr^{2})\beta)+yr(-6(2+\beta) \\& +zr^{2}(-3+(4zr^{2} -2)\beta))\bigg]\bigg[2x\sqrt{zr^{2}}(3+zr^2)(2\beta-3) \end{aligned} $

$ \begin{aligned}[b]+y(30r\beta+z^{2}r^{5}(2\beta-3) +zr^{3}(26 \beta-9))\bigg]^{-1}. \end{aligned} $

Figure 6 shows that the behavior of EoS parameters satisfy the viability condition corresponding to all the considered stellar objects.
-
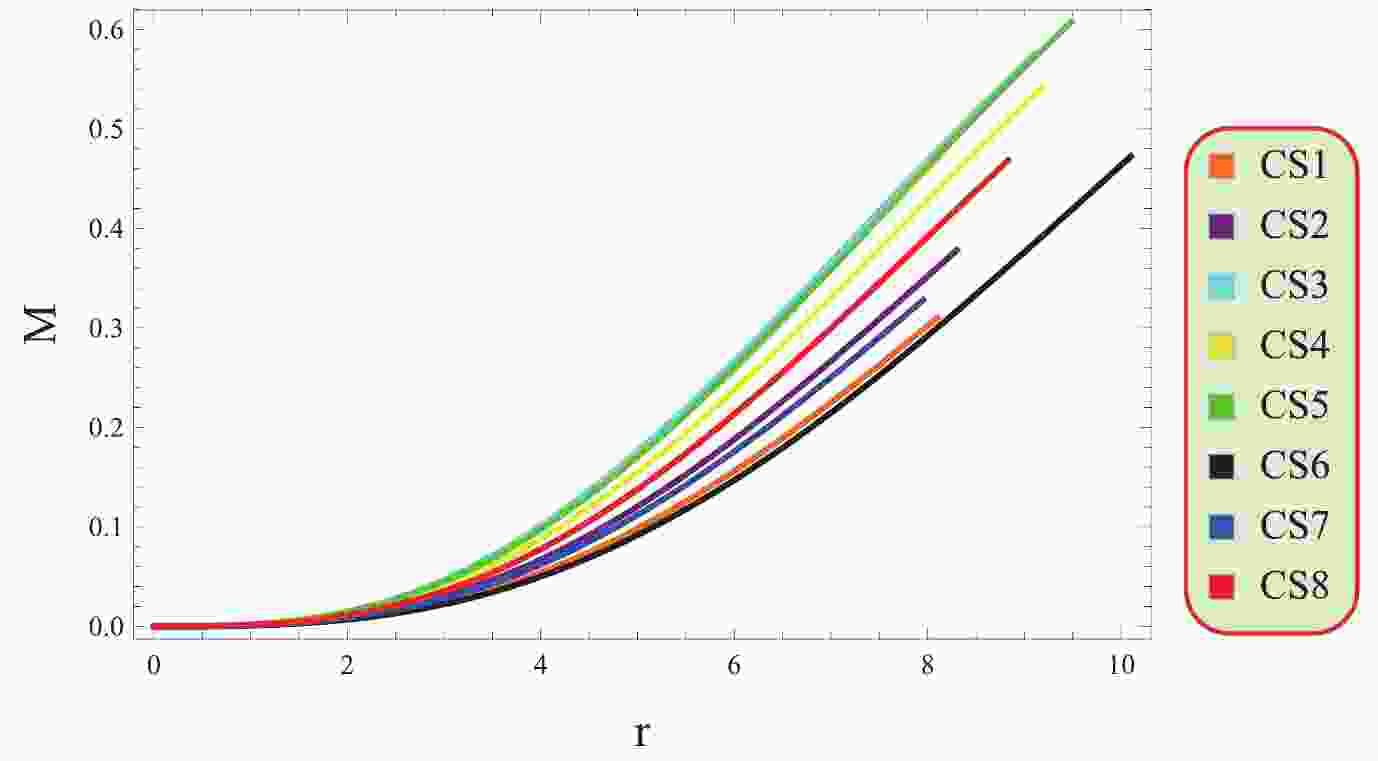
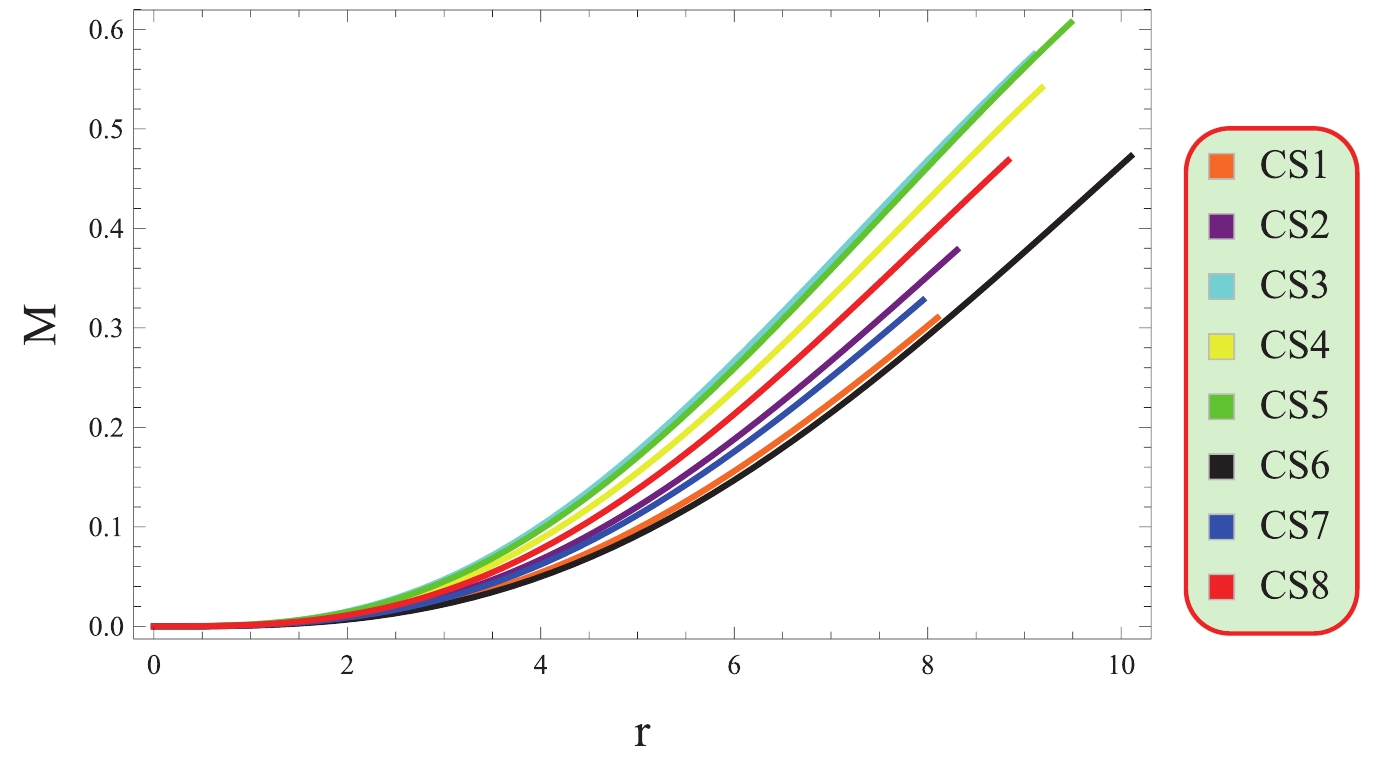
The mass of stellar objects is described as
$ M=4\pi\int^{\mathcal{R}}_{0} r^{2}\varrho {\rm d} r. $

Figure 7 demonstrates that the mass function increases monotonically and
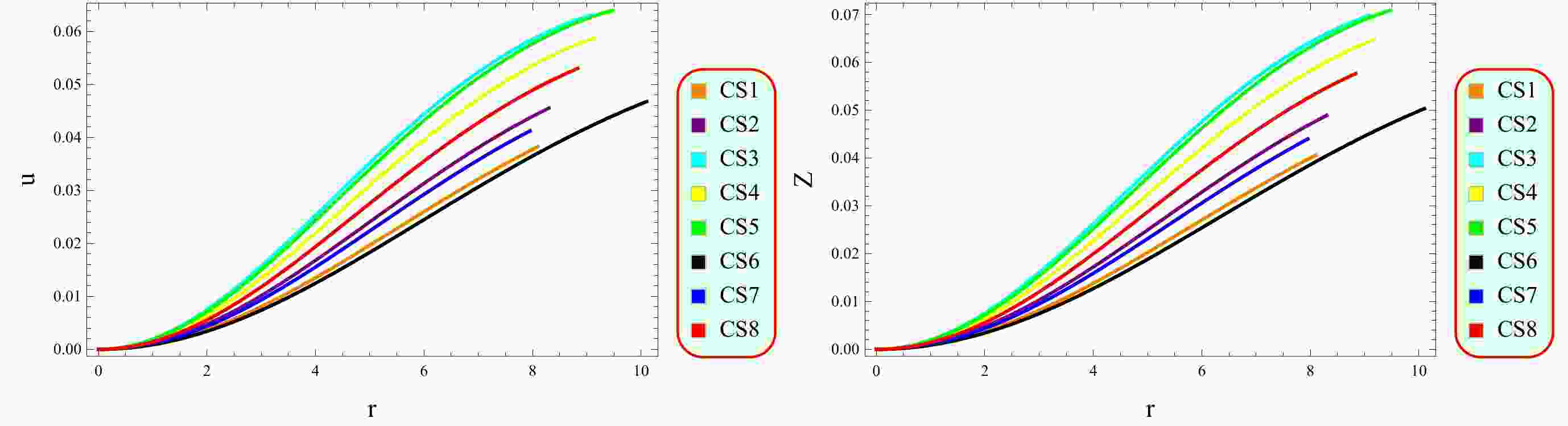
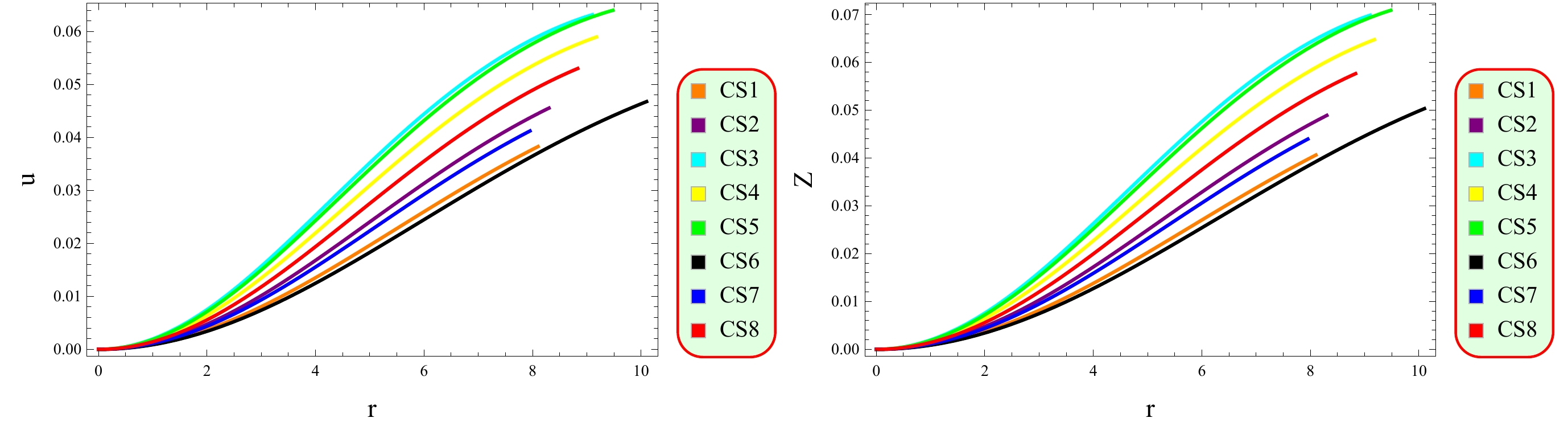
$ M\rightarrow 0 $ as$ r\rightarrow 0 $ , suggesting that the mass distribution has no irregularities. Various physical characteristics can be assessed to analyze the structural configuration of cosmic objects. A fundamental factor in assessing the viability of CSs is the compactness function, represented by$\left(u=\dfrac{M}{r}\right)$ . This function offers insights into the distribution of mass relative to the radius of a CS and its concentration. The compactness factor is a physical parameter that provides a quantitative measure of how densely packed the mass is within a given radius. There is a specific limit for the compactness function proposed by Buchdhal for a physically relevant model [58]. According to his criterion, the mass-radius ratio should be less than$ 4/9 $ for viable stellar objects.The surface redshift is a significant factor as it provides important information about the brightness and energy of light emitted from the surfaces, which is caused by the gravitational redshift due to the strong gravity. It is a phenomenon that explains the change in frequency (wavelength) of light or other electromagnetic radiations as it travels away from a gravitational field. As the light moves away from the gravitational field, it loses energy and thus its wavelength is increased, causing it to shift towards the red end of the electromagnetic spectrum. It is denoted by
$ Z_{s} $ and mathematically expressed as$ Z_s =- 1+\frac{1}{\sqrt{1-2u}}. $

(20) In the case of an anisotropic configuration, the redshift at the surface must satisfy the specific condition of
$ Z_{s}<5.211 $ for the CS to be viable [59]. The graphs in Fig. 8 demonstrate that both the compactness and redshift functions meet the essential feasibility criteria. -
It is important to comprehend the behavior and physical characteristics of celestial objects in the field of gravitational physics. The stability of cosmic formations is significant to develop their reliability and coherence. Scientists have investigated the conditions that determine the stability of these formations against various forms of oscillations. To assess the stability of pulsars, researchers use methods such as the causality constraint, Herrera cracking approach, and adiabatic index, which provide important perspectives on the structural integrity of astronomical objects.
-
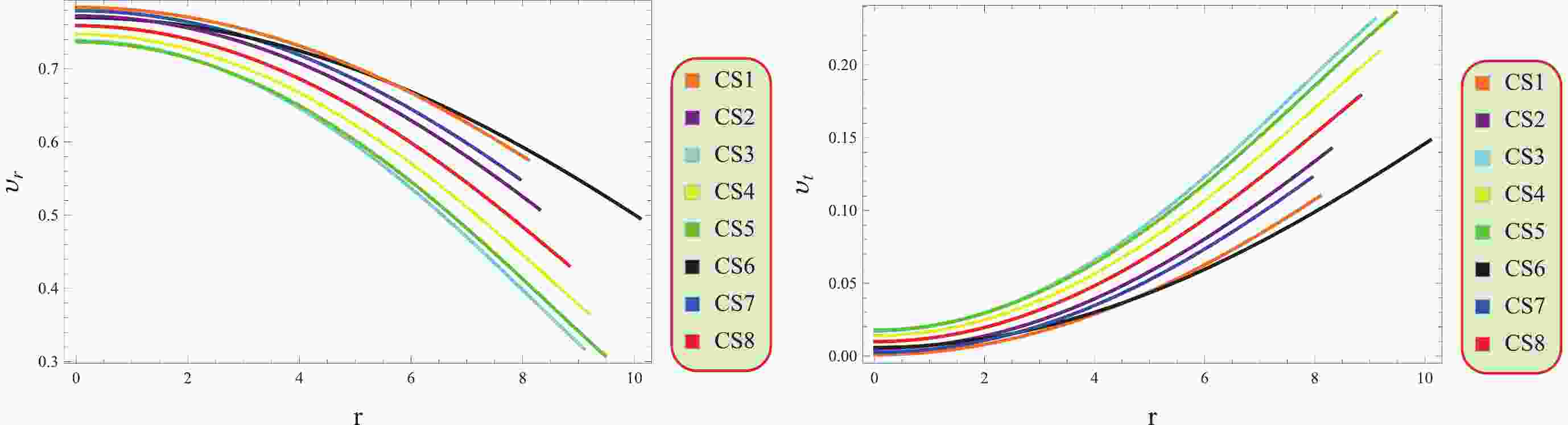
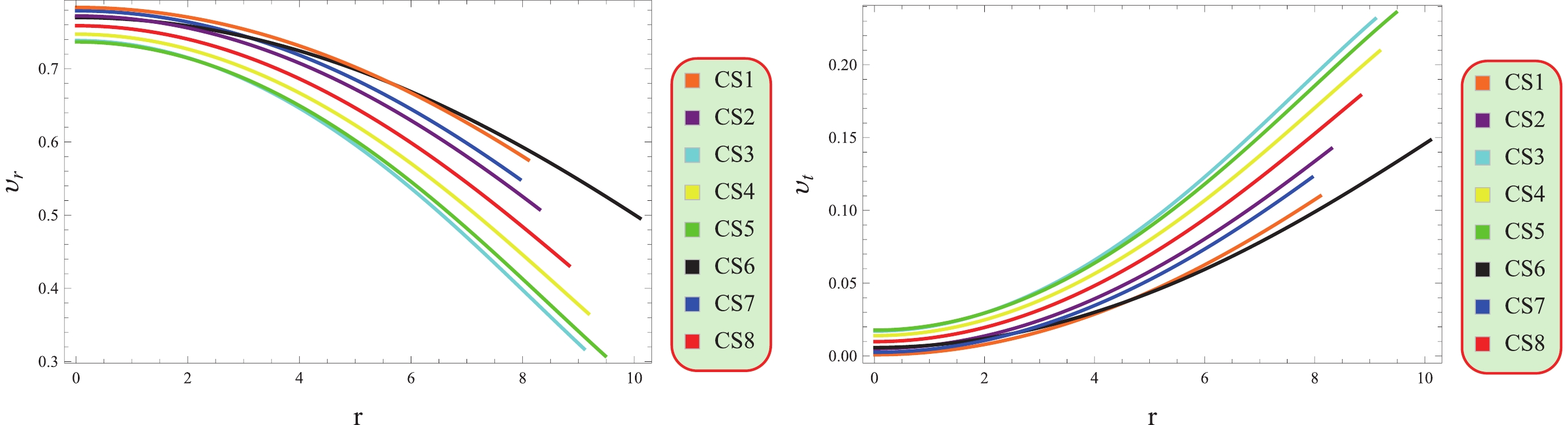
The stability of CSs can be evaluated by considering the causality constraint, which states that nothing can travel faster than the speed of light. To maintain stable configurations, both the radial and tangential velocities of sound
$\Big(v_r = \dfrac{{\rm d}p_r}{{\rm d}\varrho}$ and$v_t = \dfrac{{\rm d}p_t}{{\rm d}\varrho}\Big)$ must fall in the range of 0 to 1 [60]. These characteristics related to sound speed play a critical role in ensuring the stability of CSs. These are given as follows:$ \begin{aligned}[b] v_{r}=\;&\bigg[4x^{2}zr(3+zr^{2}(3-2\beta)+14\beta)-4xy\sqrt{zr^{2}}(6+8\beta\\&+zr^{2}(-16\beta +3+zr^{2}(2\beta-3)))-y^{2}r(6(2+\beta)\\&+zr^{2}(18(2+\beta)+zr^{2}(-22\beta +21+zr^{2}(2\beta-3))))\bigg]\\&\times\bigg[4x^{2}zr(5+zr^{2})(2\beta-3)+4xy\sqrt{zr^{2}}(20\beta \\&+z^{2}r^{4}(2\beta-3)+5cr^{2}(-3+4\beta))+y^{2}r(30\beta+zr^{2}(90\beta\\&+zr^{2}(-15 +50\beta+zr^{2}(2\beta-3))))\bigg]^{-1}, \\ v_{t}=\;&2\bigg[4x^{2}zr(3+2(2+zr^{2})\beta)+2xy\sqrt{zr^{2}}(-9-2\beta\\&+zr^{2}(3+4 (1+zr^{2})\beta))+y^{2}r(-3(2+\beta)+zr^{2}(-9(2+\beta)\\&+zr^{2}(-3+2 (-2+zr^{2})\beta)))\bigg]\bigg[4x^{2}zr(5+zr^{2})(2\beta-3)\\&+4xy\sqrt{zr^{2}}(20\beta+z^{2} r^{4}(2\beta-3)+5cr^{2}(-3+4\beta))\\&+y^{2}r(30\beta+zr^{2}(90\beta+zr^{2}(-15 +50\beta+zr^{2}(2\beta-3))))\bigg]^{-1}. \end{aligned} $

Figure 9 shows that the considered CSs satisfy the required condition. Thus, this modified theory supports the existence of physically viable and stable CSs.
-
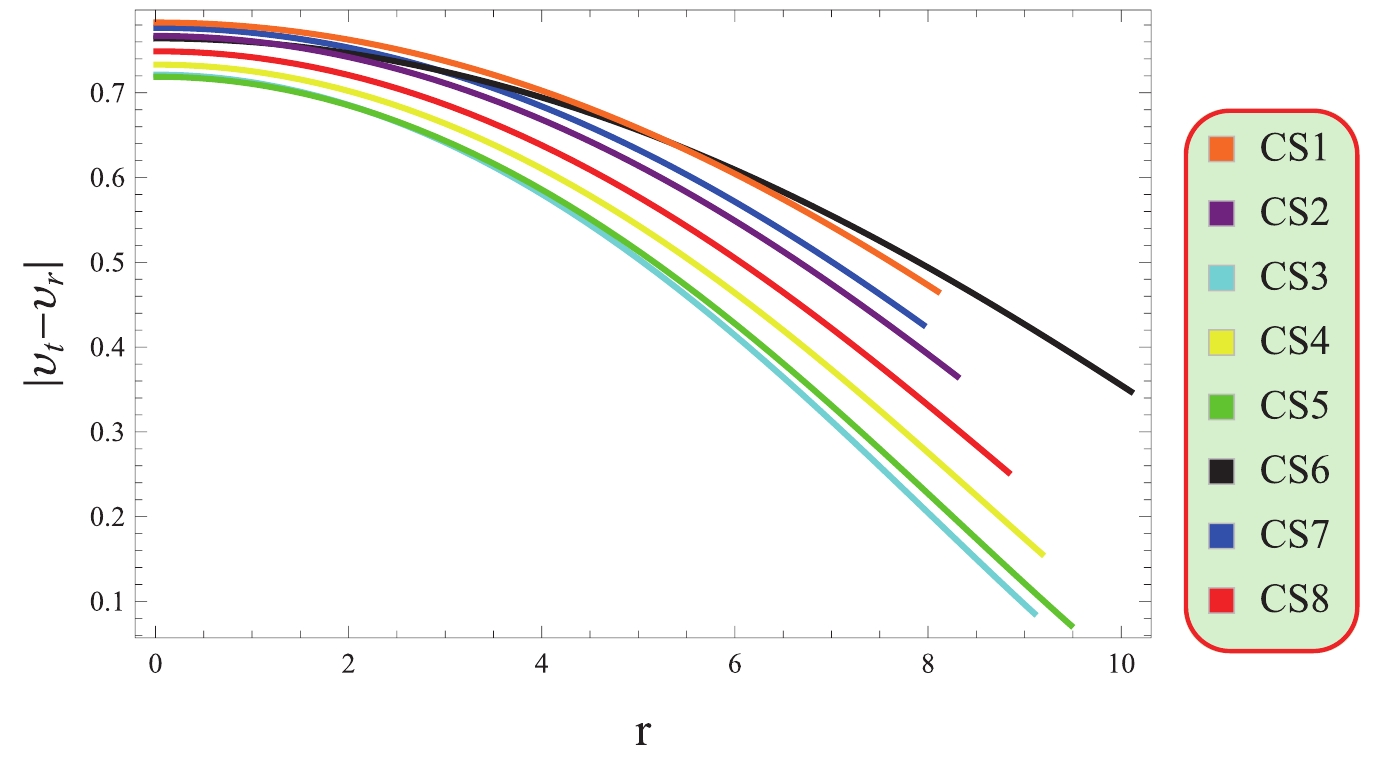
The analysis of solution's stability is based on a mathematical method called the cracking approach
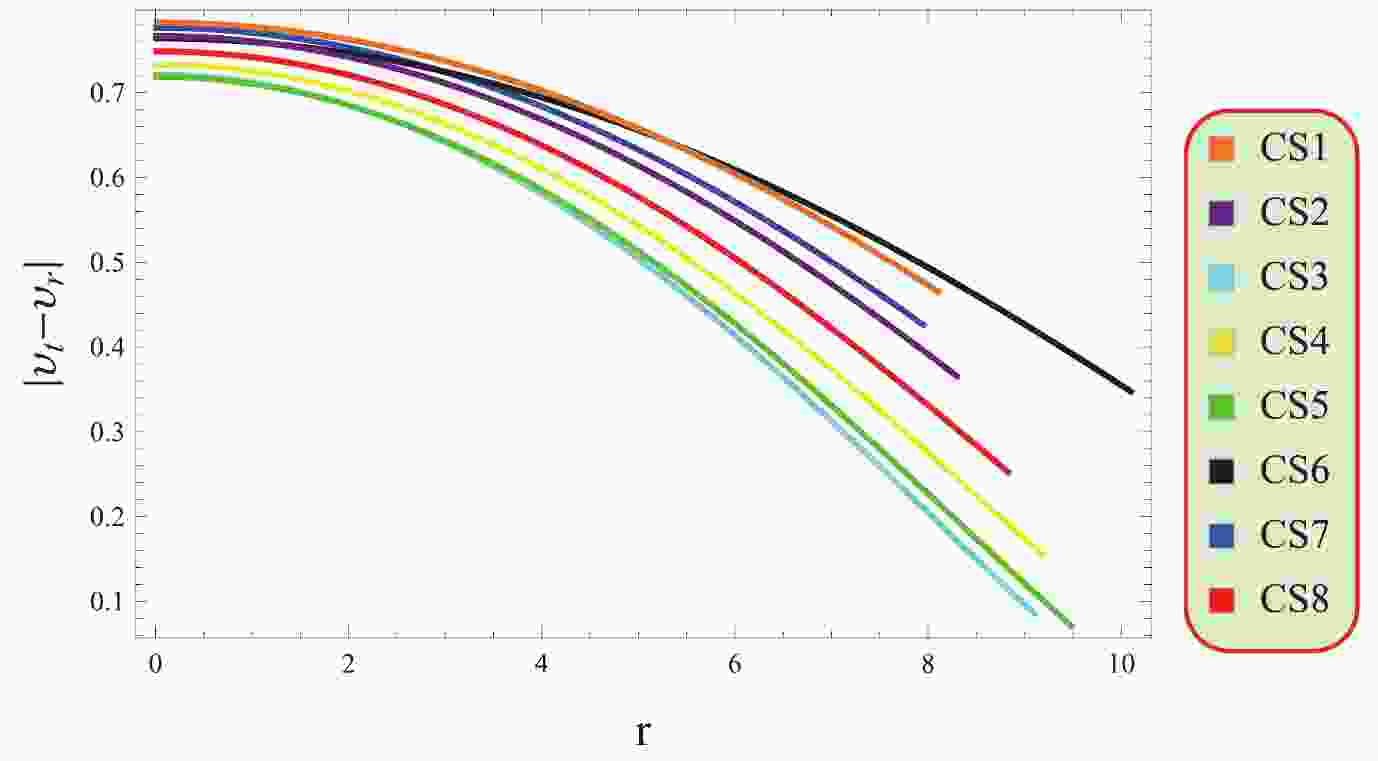
$(0\leq \mid v_{t}-v_{r}\mid\leq1)$ , which was developed by Herrera [61]. The satisfaction of this condition indicates stable cosmic structures capable of long-term existence; otherwise, it signifies instability and collapse. This method enables researchers to determine the stability of cosmic structures, which is essential for understanding their behavior in the universe. Figure 10 depicts the fulfillment of the cracking condition as both the radial and tangential sound speed components lie in the range [0, 1], which ensures the stability of the stellar objects under consideration. -
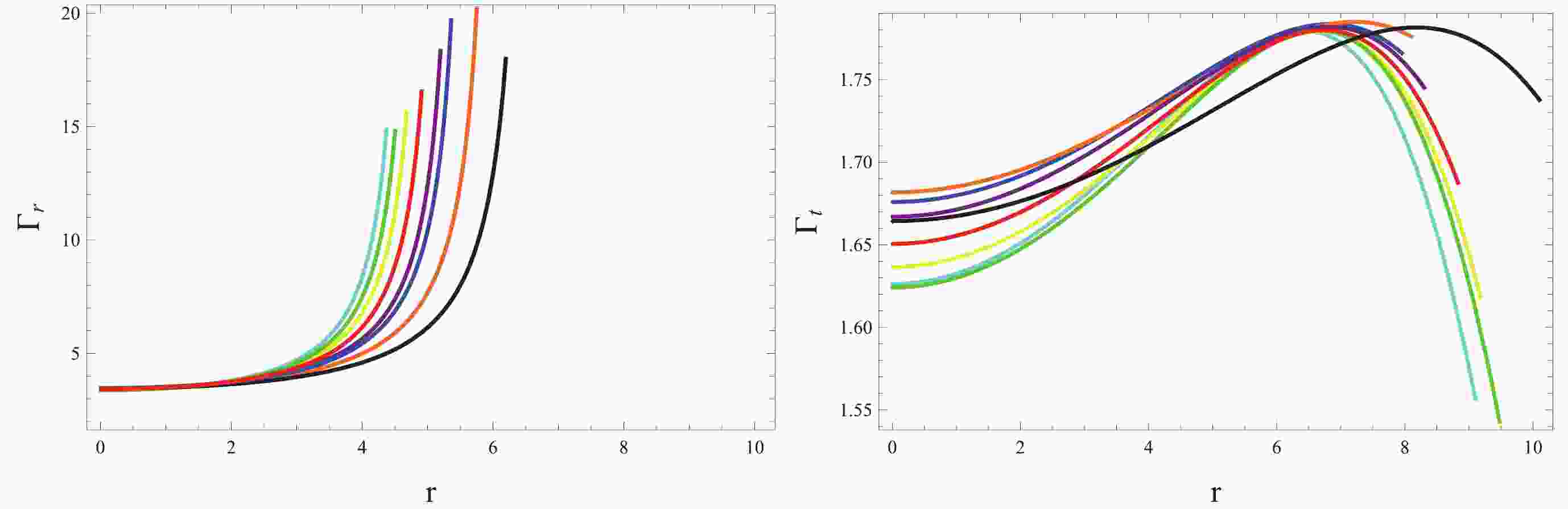
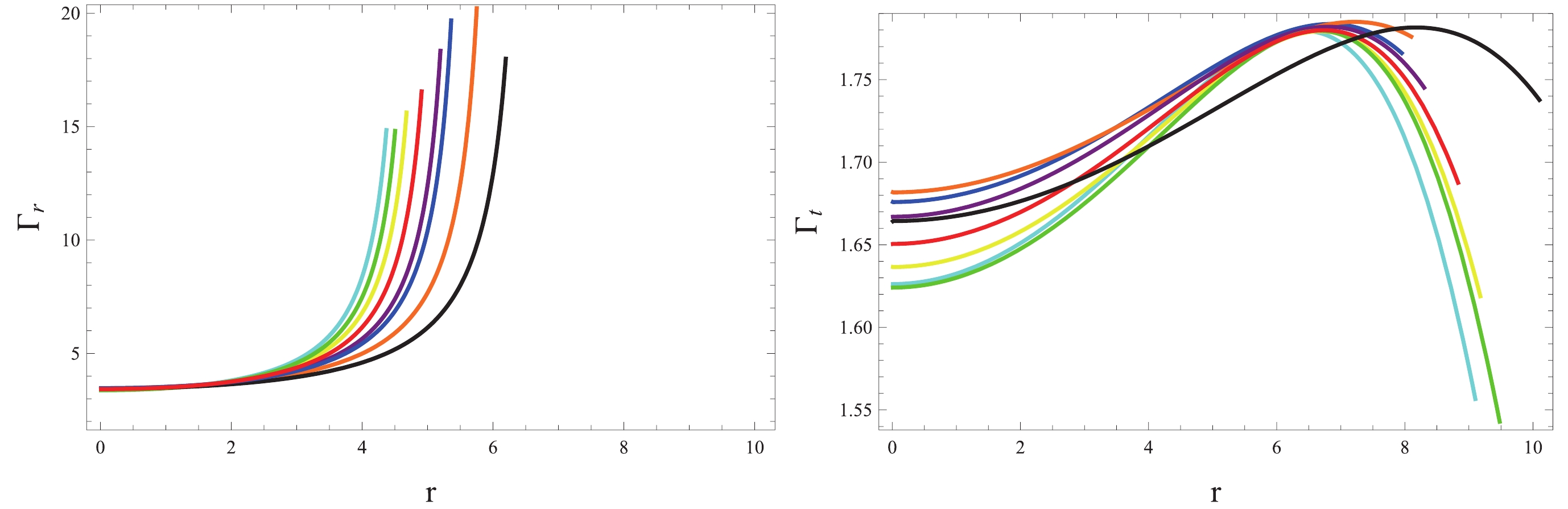
This method is considered significant to determine the stability of cosmic objects, providing insights into their composition and behavior. It characterizes how pressure changes according to density variations in stars, which plays a pivotal role in astrophysics, and is described as
$ \Gamma_{r}=\frac{\varrho+p_{r}}{p_{r}}v_{r},\quad \Gamma_{t}=\frac{\varrho+p_{t}}{p_{t}}v_{t}. $

It is essential to determine the value of Γ for the stability analysis. In a stable object, the values of Γ should be greater than 4/3, and instability leading to collapse occurs when the value falls below this limit. Figure 11 shows that our system remains stable in the presence of correction terms.
-
This study investigated the feasibility and stability of CSs in the extended symmetric teleparallel theory. The main aim was to investigate whether incorporating non-metricity into the gravitational field equations resulted in feasible solutions for CSs. Introducing these terms to the theory presents new insights into how matter and geometry interact under extreme gravitational circumstances. Furthermore, we conducted a graphical analysis of various physical characteristics to verify the viability of CSs in the proposed theoretical framework. In addition, we assessed stability through methods that incorporate the sound speed and adiabatic index.
The metric functions are essential and have a significant impact in describing the geometry of spacetime. We found that the metric coefficients are consistent and nonsingular, which ensures that the spacetime is smooth and devoid of any singularities (Fig. 1). This smoothness is a fundamental requirement for any viable cosmological model. The material contents are higher, regular, and the most concentrated at the center of the observed CSs (Fig. 2), which indicates a stable core, and this behavior of fluid parameters is desirable to maintain the structural integrity of CSs. Furthermore, the decrease in matter content towards the boundary suggests a viable distribution in the CSs. The vanishing radial pressure at the surface boundary ensures the physical viability of CSs. The matter contents exhibit a negative gradient, indicating a dense profile of the suggested stellar objects (Fig. 3).
Anisotropy vanishes at the center of CSs, which is a desirable feature for maintaining their stability (Fig. 4). Moreover, anisotropic pressure is directed outward, which is a crucial feature for compact stellar configurations. All energy constraints are positive (Fig. 5), which confirms the existence of ordinary matter in the interior of CSs. Fig. 6 indicates the viability of the considered model as the EoS parameter lies in the range of 0 and 1. The mass function (Fig. 7) remains consistent at the center of the CSs and demonstrates a steady increase as the radial coordinate increases. This behavior is indicative of a viable mass distribution in CSs. The compactness factor is less than 4/9, and the redshift is less than 5.2 (Fig. 8), supporting the viability of the compact structures. The stability limits guarantee the existence of stable CSs in this framework (Figs. 9−11).
It is worthwhile to mention here that the range of physical quantities in
$ f(Q,T) $ increases and provides more viable as well as stable compact stars as compared to GR [62−64] and other modified theories [65]. For example, in$ f(R) $ theory, it is found that physical quantities such as effective matter variables, energy conditions, EoS parameters, and speed of sound are satisfied for a very small range, and the compact star Her X-1 under the effects of the second gravity model does not remain stable [66]. In$ f(G,T) $ theory, the evolution of compact stars (SAXJ1808.4-3658 and 4U1820-30) is supported by all three gravity models, whereas for HerX - 1, some restrictions are asserted by the second model to be completely physically viable [67]. Additionally, in the framework of$ f(R,T^{2}) $ theory, it is evident that CSs are neither theoretical viable nor stable at the center [68−70]. Based on these findings, we conclude that all the CSs considered in this study exhibit both physical viability and stability at their centers in this modified theory. Consequently, our findings suggest that more viable and stable CSs can exist in this modified framework.A new class of interior solutions to the Einstein field equations for an anisotropic matter distribution using a linear EoS was presented in [70]. They verified the physical acceptability of the solutions by the current estimated data of CS 4U-160852. In contrast, our study diverges by adopting the
$f(Q,T)$ theory, a different theoretical framework that allows for a comprehensive exploration of the effects of modified terms on the viability and stability of CSs. Using distinct methodologies and techniques, we analyzed several anisotropic CSs, discerning their viability and stability under the influence of modified gravitational dynamics. Our findings reveal the feasibility of the proposed CSs even in the presence of modified terms, underscoring the robustness of our theoretical framework. By expanding the scope of our investigation to encompass a broader spectrum of CSs, we contribute to the ongoing discourse on the behavior of CSs in the alternative gravitational theory, thus enriching our understanding of astrophysical phenomena across diverse theoretical landscapes.
Stability analysis of static spherical spacetime in extended symmetric teleparallel gravity
- Received Date: 2024-05-24
- Available Online: 2024-12-15
Abstract: Our manuscript aims to analyze the viability and stability of anisotropic stellar objects in the modified symmetric teleparallel gravity. A particular model of this extended theory is considered to formulate explicit field equations that govern the interaction between matter and geometry. The configuration of static spherical symmetric structures is examined through the Finch-Skea solution. However, the values of unknown constants in the metric potentials are evaluated by the Darmois junction conditions. For the viability of the proposed stellar objects, physical parameters including density, pressure, anisotropy, mass, energy constraints, compactness function, and redshift are analyzed. Furthermore, the stability of the proposed stellar objects is investigated by the causality condition, Herrera cracking approach, and adiabatic index. Our findings indicate that the proposed stellar objects are viable as well as stable in the presence of correction terms.


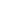
 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: