-
In the 1960s, T. R. Skyrme put forward a pioneering idea to study nucleon physics using a nonlinear theory of mesons, which was later named the Skyrme model [1, 2]. Since then, the Skyrme model and its extension have been widely used in nuclear and condensed matter physics [3–7].
The original Skyrme model is very simple. It only consists of the nonlinear sigma model term and Skyrme term, which is a combination of the
$ L_1 $ and$ L_2 $ terms in the later developed chiral perturbation theory [8]. As shown in literature, the Skyrme model has been extended for various purposes by, for example, including the pion mass, hadron resonances, or saturating the Bogomolnyi bound [9–19].It is easy to imagine that the minimal extension of the Skyrme model would involve including the pion mass term
$ m^2{\rm{Tr}}(1-U) $ [10]. The pion mass effect has been studied for several years [4, 7, 20–22]. The pion mass term has been found to affect single skyrmion properties and globally improve the results of empirical values [10]. In the multi-skyrmion system, which the current study focuses on, the pion mass strongly affects the multi-skyrmion spectrum and configurations [20, 21, 23, 24].Generally, the
$ m^2{\rm{Tr}}(1-U) $ term is not the only contributor to the pion mass. In principle, terms such as$ m^2{\rm{Tr}}(1-U^2) $ also explicitly break chiral symmetry. It is found that this term introduces a false vacuum to the Skyrme model [25–28] in addition to the vacuum of QCD. Therefore, it is interesting to study the skyrmion properties with respect to this false vacuum, which is not only relevant to hadron physics but may also help us understand the cosmological phase transition process [29–31].When this false vacuum is added, the Skyrme model admits a false meta-stable skyrmion configuration [32], which can decay due to the tunneling effect [33], consequently causing the decay of the false vacuum [25]. In addition, with the appropriate choice of the false vacuum potential, the experimental values of radii and binding energies for a wide range of nuclear mass numbers can be calculated with good precision [26–28]. In Ref. [34], multi-skyrmion properties were studied using a rational map ansatz.
In this paper, we study multi-skyrmion configurations using the product ansatz to observe the false vacuum effect on the cluster structure of nuclei. We start from the original Skyrme model [1, 2],
$ {\cal{L}}_{\rm Skyrme} = \frac{f_{\pi}^2}{16} {\rm{Tr}} \left[ \partial_{\mu} U^{\dagger} \partial^{\mu} U \right] + \frac{1}{32 e^2} {\rm{Tr}} \left[ U^{\dagger} \partial_{\mu} U, U^{\dagger} \partial_{\nu} U \right]^2, $

(1) where
$ f_\pi=184\; $ MeV, e is the Skyrme parameter, and$ U({\bf{x}})=\exp(2i\pi/f_\pi)=\exp(2i\pi^a\tau^a/f_\pi) $ , with$ \tau^a $ as the Pauli matrices.Since the chiral field
$ U(x) $ is unitary, for any fixed time, say,$ t_0 $ , the static configuration$ U({\bf{x}}, t_0) $ defines a map from the manifold$ R^3 $ to the manifold$ S^3 $ in the isospin space, that is,$ U({\bf{x}}, t_0) : R^3 \to S^3. $

(2) At the low energy limit, QCD goes to the vacuum, that is,
$ U({\bf{x}}\to \infty, t_0) = 1 $ , and all the points at$ {\bf{x}} \to \infty $ are mapped onto the north pole of$ S^3 $ . Therefore, maps (2) constitute the third homotopy group$ \pi_3(S^3) =Z $ , where the integer Z accounts for the times that$ S^3 $ is covered by the mapping$ U({\bf{x}}, t_0) $ , that is, winding numbers. Because the winding number is conserved when the time coordinate is changed and the$ N_c $ scaling of the energy of model (1) is the same as that of baryons in the constituent quark model, the solution of (1) – soliton – can be regarded as a baryon [35].In the following, for convenience, we use the energy and length scales
$ { f_{\pi} }/{4e} $ and$ { 2 }/{ef_{\pi}} $ , respectively. Using these new scales, we can rewrite the Skyrme model Lagrangian (1) as$ {\cal{L}}_{\rm Skyrme} = \frac{1}{2} {\rm{Tr}} \left[ \partial_{\mu} U^{\dagger} \partial^{\mu} U \right] + \frac{1}{16} {\rm{Tr}} \left[ U^{\dagger} \partial_{\mu} U, U^{\dagger} \partial_{\nu} U \right]^2. $

(3) Then, in the new scales, the extended Skyrme model, which includes our chosen false vacuum, has the form
$ {\cal{L}}_{\rm ESkyr} = {\cal{L}}_{\rm Skyrme} + {\cal{L}}_{\rm mass}, $

(4) where
$ {\cal{L}}_{\rm mass} ={} -\frac{1}{4} \left( m_1^2 {\rm{Tr}}\left[1-U\right] + m_2^2 {\rm{Tr}}\left[1-U^2\right] \right). $

(5) To study the effect of the false vacuum potential on the multi-skyrmions, particularly the effect of the cluster structure, we decompose the static field
$ U(x) $ as$ U( {\bf{x}} ) = \sigma + {\rm i} {\boldsymbol{\tau}} \cdot {\boldsymbol{\pi}}, $

(6) where
$ {\boldsymbol{\tau}}=( \tau_1, \tau_2, \tau_3 ) $ are the Pauli matrices, and$ {\boldsymbol{\pi}} = ( \pi_1, \pi_2, \pi_3 ) $ are the Goldstone bosons after chiral symmetry breaking. The chiral fields σ and$ \pi_i $ satisfy the constraint$ \sigma^2 + {\boldsymbol{\pi}} \cdot {\boldsymbol{\pi}} = 1. $

(7) With parameterization (6), the false vacuum potential term can be approximated as
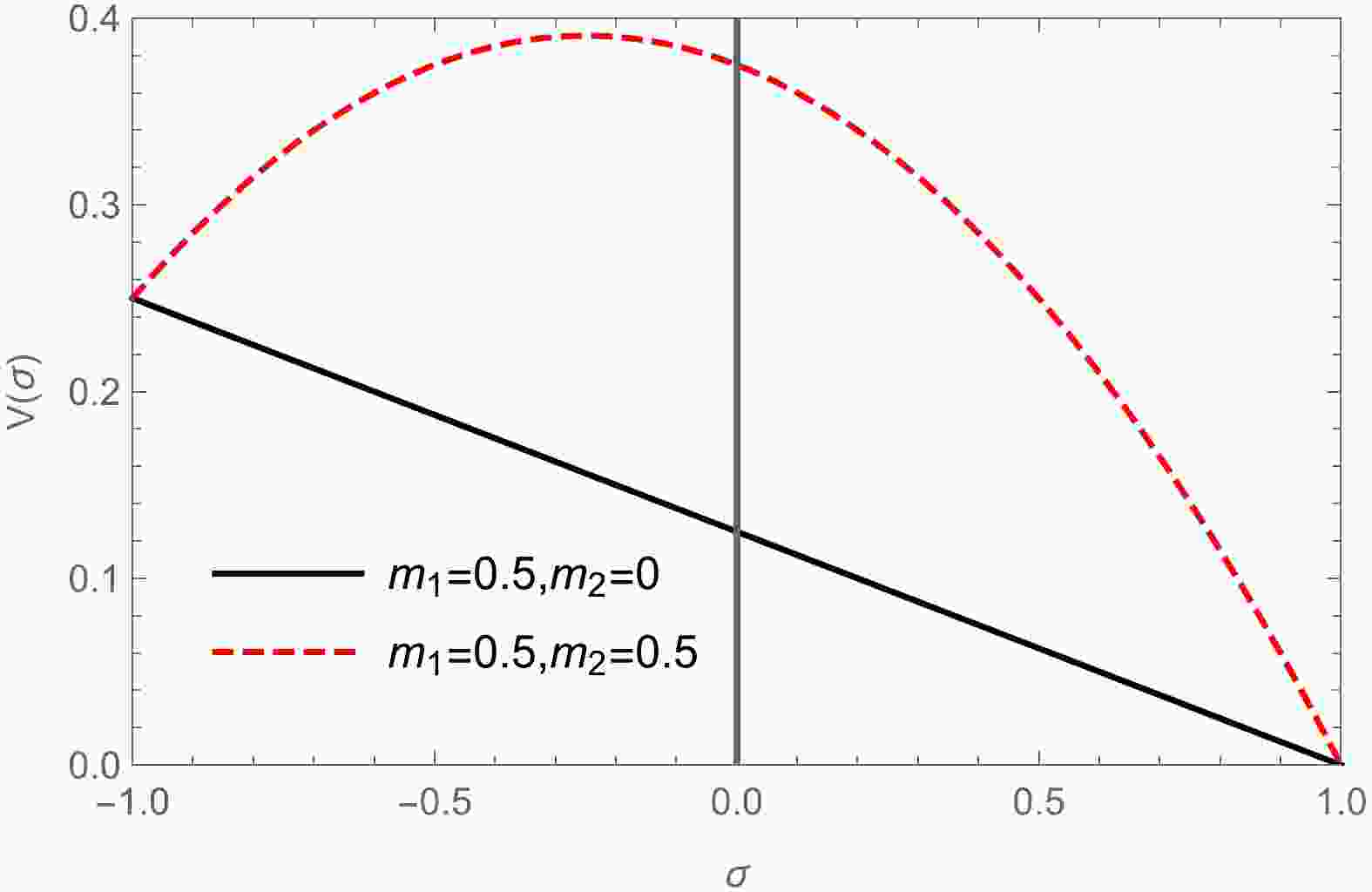
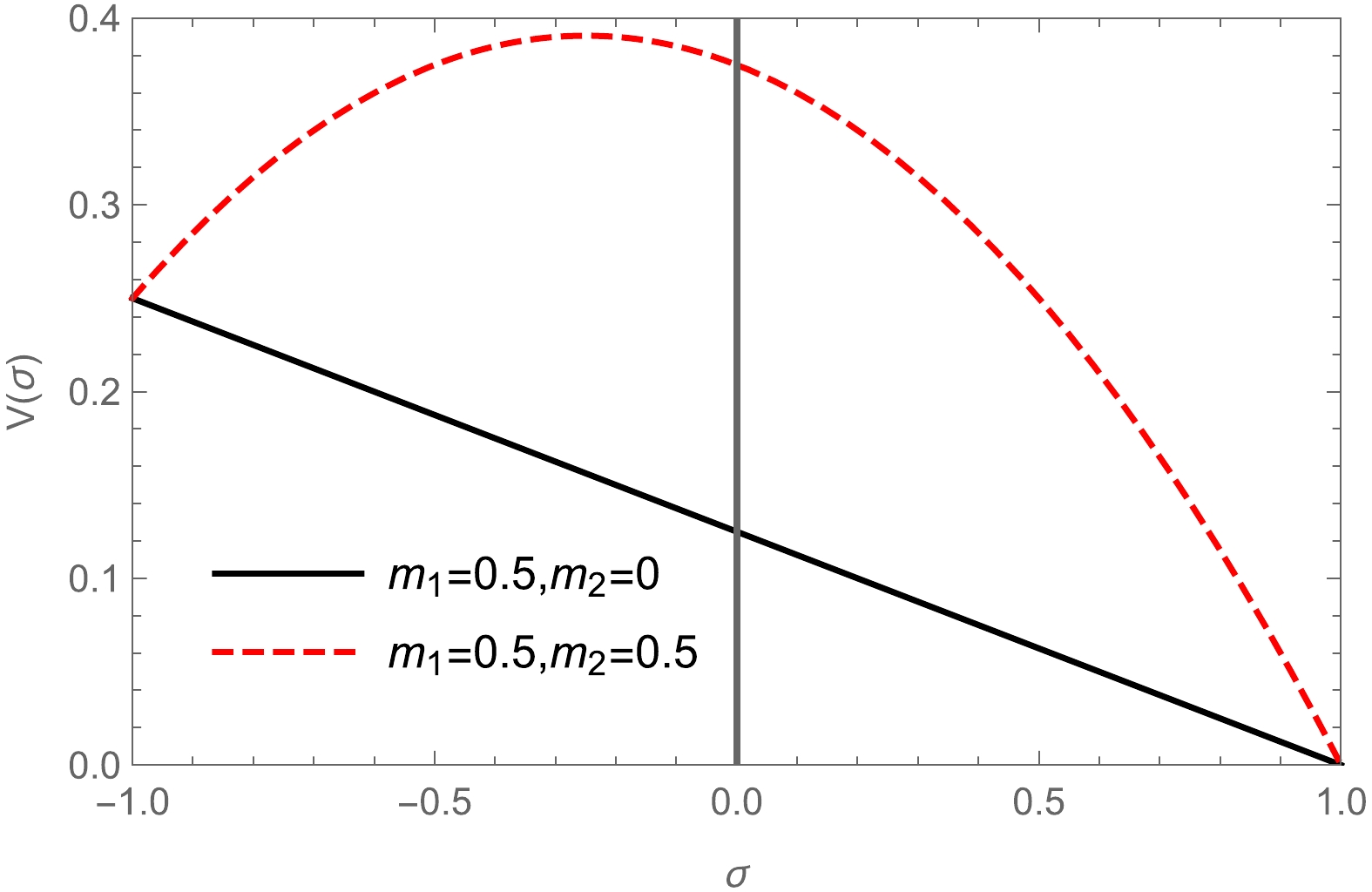
$ V = \frac{1}{2} m_1^2 (1-\sigma) + m_2^2 (1-\sigma^2). $

(8) It follows that when
$ m_1 ^2 > 4m_2 ^2 $ , for example,$m_1=0.5, m_2=0$ , there is only one global minimum located at$ U=\sigma=1 $ . However, when$ m_1 ^2 < 4m_2 ^2 $ , for example,$m_1=0.5, m_2=0.5$ , in addition to the global minimum, there is a local minimum at$ U= \sigma = {} - 1 $ . This is illustrated in Fig. 1. It should be noted that due to the quantum tunneling effect, the local minimum is metastable.From Lagrangian (4) and using parameterization (6), we obtain the Hamiltonian of the system as
$ \begin{aligned}[b] H = & \int {\rm d}^3x \Big \{ \partial_{i} \sigma \partial_i \sigma + \partial_{i} \vec{\pi} \cdot \partial_i \vec{\pi} \\ & - \frac{1}{2} \left( \partial_{i} \sigma \partial_j \sigma + \partial_{i} \vec{\pi} \cdot \partial_j \vec{\pi} \right) \left( \partial_{i} \sigma \partial_j \sigma + \partial_{i} \vec{\pi} \cdot \partial_j \vec{\pi} \right) \\ & +\frac{1}{2} \left( \partial_{i} \sigma \partial_i \sigma + \partial_{i} \vec{\pi} \cdot \partial_i \vec{\pi} \right) \left( \partial_{j} \sigma \partial_j \sigma + \partial_{j} \vec{\pi} \cdot \partial_j \vec{\pi} \right) \\ & + V_{\rm eff} \Big \}, \end{aligned} $

(9) where, for convenience, we introduce the effective potential
$V_{\rm eff}$ as$ V_{\rm eff} \equiv \left\{\begin{array}{*{20}{l}} {V,}& {U(\infty)= + 1\; ( {\rm{skyrmions}} )}\\{V-m_1^2,} &{U(\infty)= - 1\; ( {\rm{false \;skyrmions}} ) }\end{array}\right. $

(10) which satisfies
$V_{\rm eff}\to 0$ as$ {\bf{x}} \to \infty $ .We next study the effect of the false vacuum potential on the multi-skyrmion configurations using the product ansatz. The basic idea of product ansatz can be summarized as follows: Given two
$S U(2)$ symmetric fields and the skyrmion solutions, the one with baryon number$ B_1 $ , referred to as$ U_1 ({\bf{x}}_1) $ , and the other with baryon number$ B_2 $ , referred to as$ U_2 ({\bf{x}}_2) $ , we can construct a new skyrmion configuration$ U({\bf{x}}) $ with baryon number$ B=B_1 + B_2 $ by multiplying them together. To find the lowest energy configuration of the new skyrmion$ U({\bf{x}}) $ , the two original skyrmions are placed with a relative rotation in the isospin space,$ U({\bf{x}}) = U_1 ({\bf{x}}_1) C({\boldsymbol{\alpha}}) U_2 ({\bf{x}}_2) C ^\dagger({\boldsymbol{\alpha}}) \equiv U_1 ({\bf{x}}_1) U_2^\prime ({\bf{x}}_2), $

(11) where
$C({\boldsymbol{\alpha}}) ={\rm{exp}} ( {\rm i} {\boldsymbol{\tau}} \cdot {\boldsymbol{\alpha}} /2 ) = {\rm{exp}} ( {\rm i} {\boldsymbol{\tau}} \cdot \hat{ {\boldsymbol{\alpha}} } \alpha /2 )$ , representing a rotation of α angles around the$ \hat{ {\boldsymbol{\alpha}} } $ -axis in the isospin space. The direction of the$ \hat{{\boldsymbol{\alpha}}} $ -axis and the magnitude of the rotation angle α are determined by minimizing the energy of the system which a physical system should satisfy. Using parameterization (6), the new$ U^\prime $ field after rotation is expressed as$ U^\prime({\bf{x}}) = \sigma' + {\rm i} {\boldsymbol{\tau}} \cdot {\boldsymbol{\pi}}'( {\bf{x}} ) $

(12) where
$ \begin{aligned}[b]\sigma^\prime =& \sigma, \\ {\boldsymbol{\pi}}^\prime =& ( {\boldsymbol{\pi}} \times \hat{ {\boldsymbol{\alpha}} } ) \sin \alpha + {\boldsymbol{\pi}} \cos \alpha + \hat{ {\boldsymbol{\alpha}} } {\boldsymbol{\pi}} \cdot \hat{ {\boldsymbol{\alpha}} } ( 1-\cos \alpha ). \end{aligned} $

(13) The multi-skyrmion states are obtained by varying the rotation angle and distance between the initial states.
In the numerical calculation below, to find the energy minima of the multi-skyrmions system, the finite element method [36] is used to solve the three-dimensional partial differential equation generated from a variation of Eq. (9), with an additional Lagrange multiplier λ in constraint (7). The equation of motion is implicated in numerical calculation through the minimization of the energy constrained by the boundary conditions. Therefore, our calculation is a three-dimensional simulation.
The initial values of the multi-skyrmion solutions are constructed using the product ansatz [37, 38]. Explicitly, the initial value of the baryon number
$ B=2 $ state is constructed using the solutions of the two$ B=1 $ states– clusters–which are far away from each other. The relative rotation of the two clusters is found to have an angle π along the axes perpendicular to the line connecting the two clusters. Similarly, for the baryon number$ B=4 $ state, its initial value is obtained by producting the previous solutions of the$ B=2 $ skyrmions. However, since the$ B=2 $ clusters are not ideal spheres, the relative rotations between them are complicated. To have the strongest attraction, the two clusters should rotate at an angle π along the axis perpendicular to the line crossing the holes of the two donuts, as shown in Fig. 2a. The initial value of the baryon number$ B=8 $ state is constructed from two skyrmions of$ B=4 $ with relative rotation$ \pi/2 $ , as shown in Fig. 2b.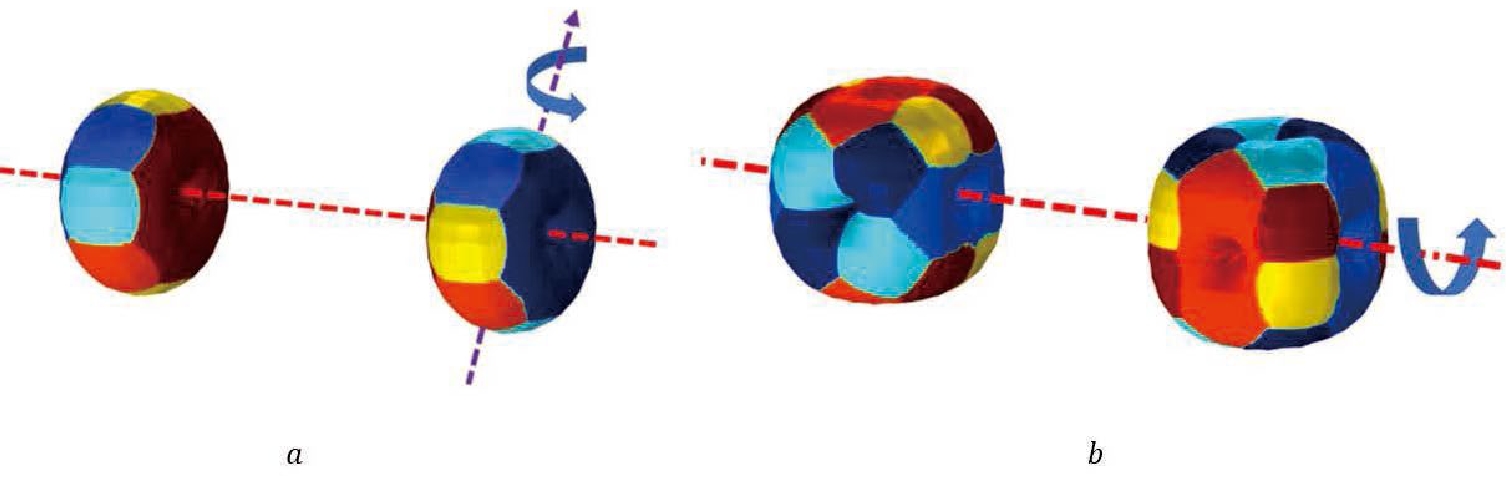
Figure 2. (color online) Relative rotations of the
$ B=2 $ clusters (left panel) and$ B=4 $ clusters (right panel).It should be noted that the initial value of the multi-skyrmion state can also be obtained using the values of each cluster given by the rational map ansatz [39]. The relative rotation between the two clusters is found to be the same as that in the product ansatz. The final results obtained from these two approaches agree with each other.
The use of the product ansatz only offers the initial value of the multi-skyrmion state with the two clusters far away from each other. A possible way to obtain the bound state in the attractive channel is to approach the two clusters by adding a pseudo-time component to the static configuration, a method known as the relaxation method [37, 38]. Here, we use a simpler method to reduce the distance by squeezing the original configuration. This method can be understood as follows using a one-dimensional ansatz: Let the size of the final multi-skyrmion state with profile
$ f(x) $ be L, the size of each cluster be$ L/2 $ , and the center of the two clusters be the origin. In the next iteration, the size of the one-dimensional soliton becomes$ L - dl $ , the size of each cluster is$ L/2-dl/2 $ , and the profile function in the next iteration can be defined as$ f^\prime(x) = \left\{ \begin{array}{*{20}{l}} {f\left( x - \dfrac{dl}{2} \right),} & {-\dfrac{L}{2}+\dfrac{dl}{2} \le x < -\dfrac{L}{4} + \dfrac{dl}{2}} \\{f\left( \dfrac{L}{L-2dl} x \right), }& {|x| \le \dfrac{L}{4} - \dfrac{1}{2} dl }\\{f\left( x + \dfrac{dl}{2} \right), }& {\dfrac{L}{4}-\dfrac{dl}{2} < x \le \dfrac{L}{2}-\dfrac{dl}{2}} \end{array}\right. . $

(14) Via this method, the size of the solitons decreases by
$ dl $ for each iteration. The final profile is obtained until the energy minimum is accessed. In this study, the two clusters of skyrmions are aligned in the x-direction, and the parameters$ dl=0.02 $ and$ dl=0.05 $ are used to obtain the minimum.To show the effect of the mass parameters on the multi-skyrmion configurations, we use four typical combinations:
●
$ m_1 = m_2 = 0.5 $ : Skyrme model with a false vacuum.●
$m_1 =0, \;m_2 = 0.5$ : Skyrme model with a false vacuum.●
$m_1 =0.5, \;m_2 = 0$ : Skyrme model with massive pions.●
$ m_1 = m_2 = 0 $ : Skyrme model in the chiral limit.Figure 3 shows the contour surface of baryon number density with
$ m_1 = m_2 = 0.5 $ for multi-skyrmion states with baryon numbers$ B=2,4,8 $ . For baryon numbers$ B=2,4 $ , the symmetries of false skyrmions calculated in this study (see Fig. 3a and Fig. 3b) are the same as those of true skyrmions [39]. However, for the multi-skyrmion state with baryon number$ B=8 $ , we obtain two configurations using$ dl=0.02 $ (Fig. 3c) and$ dl=0.05 $ (Fig. 3d), corresponding to the truncated octahedron solution and$ D_{4h} $ solution, respectively. The latter can be regarded as a bound state consisting of two cubic skyrmions with$ B=4 $ . In our calculation, the$ D_{4h} $ solution is a local minimum, whereas the truncated octahedron solution is a global minimum.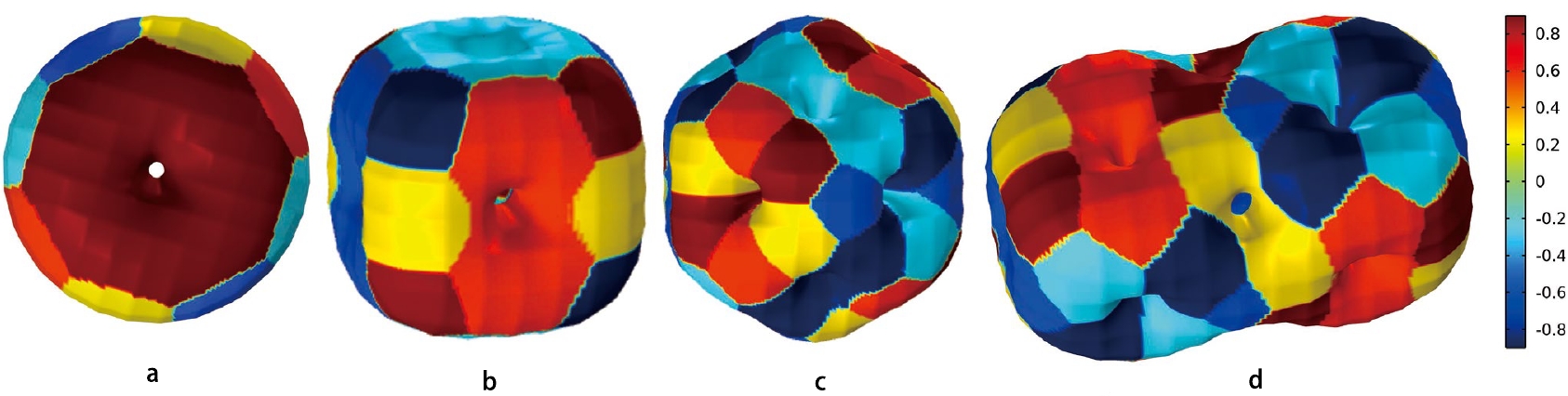
Figure 3. (color online) Baryon number density
$ {\cal{B}}^0=0.02 $ contour suface for a false vacuum$ m_1=m_2=0.5 $ . The colors encode the largest magnitude and sign of the three constituent pion fields. a: false skyrmions with$ B=2 $ . b: false skyrmions with$ B=4 $ . c: truncated octahedron false skyrmions with$ B=8 $ . d:$ D_{4h} $ false skyrmions with$ B=8 $ .Although the two configurations of the
$ B=8 $ state with$ m_1=m_2=0.5 $ depend on the choice of$ dl $ , this phenomenon does not occur for other sets of mass parameters, at least for the two values of$ dl $ chosen. This is confirmed by the calculation with the other three sets of mass parameters, as shown in Fig. 4. It is also worth noting that for the mass parameters$m_1=0, \;m_2=0.5$ , as shown in Fig. 4a, the two clusters are closer than those in the other two sets and have a more prominent contact. Moreover, in the case of the mass parameters$m_1=0, \;m_2=0$ , that is, in the standard Skyrme model, the skyrmion solution with the baryon number$ B=8 $ has two clusters with$ B=4 $ (Fig. 4c). This cluster structure of the$ B=8 $ multi-skyrmion states may arise from the product ansatz used here. As studied in Ref. [23], the truncated octahedron structure may have a lower energy when using the rational map approach.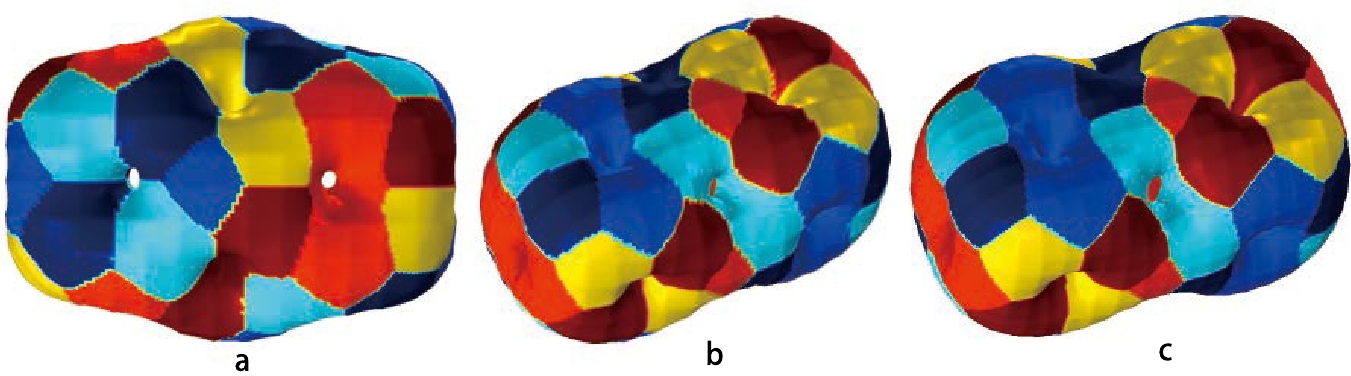
Figure 4. (color online) Baryon number density
$ {\cal{B}}^0=0.02 $ contour suface for the$ B=8 $ state. a: false skyrmions with$ m_1=0, $ $ m_2=0.5 $ ; b: skyrmions with$ m_1=0.5,\; m_2=0 $ ; c: skyrmions with$ m_1=0,\; m_2=0 $ .Table 1 shows the energy of the multi-skyrmion system with different choices of mass parameters. We can clearly see that the inclusion of the explicit chiral symmetry breaking effect increases both the masses of the multi-skyrmion states and decreases the binding energies. It should be noted that with all the parameter choices, bound states exist.
B $m_1=0.5$ 

$m_1=0$ 

$m_1=0.5$ 

$m_1=0$ 

$m_2=0.5$ 

$m_2=0.5$ 

$m_2=0$ 

$m_2=0$ 

1 1.27 1.29 1.25 1.23 2 2.48 2.51 2.46 2.42 4 4.56 4.62 4.54 4.47 8 8.91/9.00 8.95 9.20 8.86 Table 1. Energy for multi-skyrmion states (scale:
$ 12\pi^2\cdot f_\pi/4e $ ).In summary, in this study, we add a false vacuum potential term to the Skyrme model and focus on the masses and baryon number density distributions of multi-skyrmion states up to baryon number
$ B=8 $ . We find that using the product ansatz, both the false and true vacuum potentials can result in cluster structures for the multi-skyrmion states. With certain mass parameters, the conclusion may differ from this when using the rational map ansatz. This issue should be clarified in detail in the future. -
We would like to thank Y. Tian and H. B. Zhang for valuable discussions.
Multi-skyrmion states in the Skyrme model with a false vacuum potential
- Received Date: 2023-05-02
- Available Online: 2023-09-15
Abstract: We study multi-skyrmion states using the Skyrme model with a false vacuum potential up to baryon number



 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: