-
Spontaneous nuclear radioactivity embracing α decay, proton radioactivity, and cluster radioactivity has constantly been regarded as a vital channel to explore the nuclear structures of heavy and superheavy nuclei [1–8]. Cluster radioactivity, as one of the most important decay modes [9, 10], has been a prominent topic [11] since its first theoretical prediction was proposed by Sǎndulescu, Poenaru, and Greiner in 1980 [12] and experimental confirmation was realized from observing 14C emitted from 223Ra by Rose and Jones in 1984 [13]. This exotic decay mode, known as an intermediate physical process between α decay and spontaneous fission [14, 15], is generally dealt with via two main types of approaches: α-like and fission-like models [16–19]. For the former, the emitted cluster is considered pre-born in the parent nucleus before it penetrates the interacting potential barrier with different preformation probabilities [20–23]. For the latter, the emitted cluster is assumed to be formed along with the constant geometric shape deformations occurring in its nuclear barrier penetration process from the parent nucleus to the scission configuration within Gamow's penetration theory [24–26]. Essentially, the α-like and fission-like models are equivalent because the cluster preformation probability in the α-like model is interpreted as the penetrability of the pre-scission part of the nuclear barrier in the fission-like model [27].
Moreover, with the development of α decay and cluster radioactivity exploration, intensive phenomenological semi-empirical relationships based on the above theoretical approaches and/or models, as generalizations of the striking law of half-lives in logarithmic form and the decay energy in the case of α decay proposed by Geiger and Nuttall [28, 29], have been effectively applied to the investigation of cluster radioactivity [30–34] because they both share the quantum tunneling mechanism. For instance, in 2004, Ren et al. extended the famous Viola-Seaborg formula from α decay [35, 36] to complex cluster radioactivity (EVS) [37]. Later, derived from the WKB barrier penetration probability with several approximations, Ni et al. proposed a unified formula for the half-lives of both α decay and cluster radioactivity [38]. In 2009, using the microscopic mechanism of charged-particle emission, Qi et al. proposed a universal decay law for charged-particle radioactivity including α decay and cluster radioactivity based on α-like R-matrix theory [39]. In 2011, Poenaru proposed a single universal curve based on fission-like theory for α decay and cluster radioactivity (UNIV) [40]. These formulas successfully contribute to describing cluster radioactivity half-lives.
Over the past years, systematic theoretical reinvestigation has been conducted on α decay owing to special interest in studies on superheavy nuclei and cluster radioactivity [41, 42]. The advancing progress of experimental techniques and infrastructures has enabled an increasing number of cluster members ranging from 14C to 34Si, decaying from 221Fr to 242Cm with the daughter nuclei usually being the doubly magic nucleus 208Pb or its neighboring nucleus [43, 44], to be availably observed in experiments [45, 46]. Simultaneously, cluster radioactivity experimental data have been accumulated with adequately accurate precision so that their systematics can be explored almost independently of a model. Nevertheless, all analyses or predictions of cluster radioactivity half-lives undertaken to date were mostly dependent on theoretical models. The prescriptions of these models and/or the physical meaning of the parameters used by them have been subjected to criticism to various degrees [47].
Consequently, a number of model-independent semi-empirical formulas were established to evaluate the half-lives of cluster radioactivity, which were directly derived from experimental facts dependent on cluster radiaoactivity half-lives. In 2004, Horoi et al. proposed a scaling law underlining the most important variables that scale the cluster radioactivity probabilities [47]. Before long, Balasubramaniam and his collaborators put forward a semi-empirical formula based on experimental facts, which had only three parameters with a root-mean-square (rms) deviation
$ \sigma=0.89 $ [48]. However, there are still large deviations between experimental cluster radioactivity half-lives and the theoretically calculated values obtained using these formulas. It is necessary to probe more new physical factors critical to cluster radioactivity half-lives, such as the parent nucleus mass, to improve the accuracy. To this end, in the present study, we systematically analyze the effect of the parent mass on cluster radioactivity half-lives and find that there is a linear relationship between cluster radioactivity half-lives and the parent nucleus mass. Furthermore, based on Balasubramaniam's work, considering the effect of the parent mass nucleus, blocking effect, and effect of reduced mass on cluster radioactivity half-lives, we propose a new Geiger-Nuttall (G-N) law that is model-independent to calculate cluster radioactivity half-lives.This article is organized as follows. The detailed theoretical framework of the phenomenological semi-empirical formula of cluster radioactivity half-lives is presented in Sec. II. Numerical results and detailed discussion are given in Sec. III. Finally, Sec. IV contains a brief summary.
-
In 1911, Geiger and Nuttall first observed the linear relationship between the α decay half-life and Q-value and proposed the G-N law, which can be expressed as [49]
$ \log_{10} (T_{1/2})=aQ^{-1/2}+b, $

(1) where a and b are two adjustable parameters dependent on different α decay radioactive isotopes, which makes it difficult to universally describe all α decay cases using this formula and results in a limited predictive power. In 2000, considering the effect of the parent nucleus mass and charge on α decay half-lives, Royer generalized the G-N law to estimate the half-lives of all α decay cases in a uniform form. This can be written as [50]
$ \log_{10} (T_{1/2})=a\frac{Z}{\sqrt{Q_{\alpha}}}+bA^{1/6}Z^{1/2}+c, $

(2) where Z and A are the charge and mass number of the parent nucleus,
$ Q_{\alpha} $ is the α decay energy, and a, b, and c are the adjustable parameters for different types of parent nuclei. The corresponding values of these parameters are given as follows:Case I for even-even nuclei: a=−25.31, b=−1.1629, c=1.5864;
Case II for even-odd nuclei: a=−26.65, b=−1.0859, c=1.5848;
Case III for odd-even nuclei: a=−25.68, b=−1.1423, c=1.592;
Case IV for odd-odd nuclei: a=−29.48, b=−1.113, c=1.6971.
However, several physical factors in contrast with α decay should be considered differently when generalizing the G-N law to describe the half-lives of cluster radioactivity in spite of the two similar physical processes. For instance, in 2004, Horoi proposed the first model-independent scaling law for the half-lives of α decay and cluster radioactivity [47], which can be expressed as
$ \log_{10} (T_{1/2})=(a_{1}\mu^{x}+b_{1})\left[\frac{(Z_{e}Z_{d})^{y}}{\sqrt{Q}}-7\right]+(a_{2}\mu^{x}+b_{2}), $

(3) where
$ Z_{e} $ and$ Z_{d} $ are the charge number of the emitted α particle and/or cluster and daughter nucleus, respectively,$ a_{1} $ =9.1,$ b_{1} $ =−10.2,$ a_{2} $ =7.39,$ b_{2} $ =−23.2, x=0.416, and y=0.613 are the parameters adjusted by fitting the experimental data of 119 α decays and 11 cluster radioactivities emitted from even-even parent nuclei, and Q is the decay energy of α decay and/or cluster radioactivity. In the study, the effect of the reduced mass μ on both α decay and cluster radioactivity half-lives was systematically investigated. The results indicated that μ is sensitive to the half-lives of cluster radioactivity, whereas it has less effect on α decay half-lives.In addition, a recent study reported that cluster radioactivity half-lives increase as the size of the emitted cluster increases [32, 38]. Therefore, the mass number (
$ A_{c} $ ) and charge number ($ Z_{c} $ ) of the emitted cluster are crucial factors in the investigation of cluster radioactivity half-lives. Meanwhile, because the same cluster is emitted from different parent nuclei, the mass asymmetry ($ \eta = \dfrac{A_{d}-A_{c}}{A} $ , where$ A_{d} $ is the mass number of the daughter nucleus) and charge asymmetry ($ \eta_{z} = \dfrac{Z_{d}-Z_{c}}{Z} $ , where$ Z_{c} $ is the charge number of the emitted cluster) should be further explored. In 2004, considering the above two experimental factors, Balasubramaniam et al. put forward a new model-independent formula, which is expressed as [48]$ \log_{10} (T_{1/2})=\frac{aA_{c}\eta+bZ_{c}\eta_{z}}{\sqrt{Q_{c}}}+c, $

(4) where
$ Q_{c} $ is the cluster radioactivity decay energy, and a=10.603, b=78.027, and c=−80.669 are the adjustable parameters.Generally, the structures of the ground states of odd-
A and odd-odd nuclei are naturally different from those of even-even nuclei because of the unpaired nucleon which hinders the transition of these states, a process known as the blocking effect associated with the preformation probability [37]. Moreover, the larger this hindrance, the smaller the preformation probability, and a smaller preformation probability results in a prolonged cluster radioactivity half-life [28]. Therefore, the blocking effect is another critical factor in the calculation of cluster radioactivity half-lives. Based on the above discussion, considering the effect of the parent nucleus mass, effect of mass and charge asymmetries, blocking effect, and effect of reduced mass on cluster radioactivity half-lives, we propose a new G-N law for cluster radioactivity half-lives. -
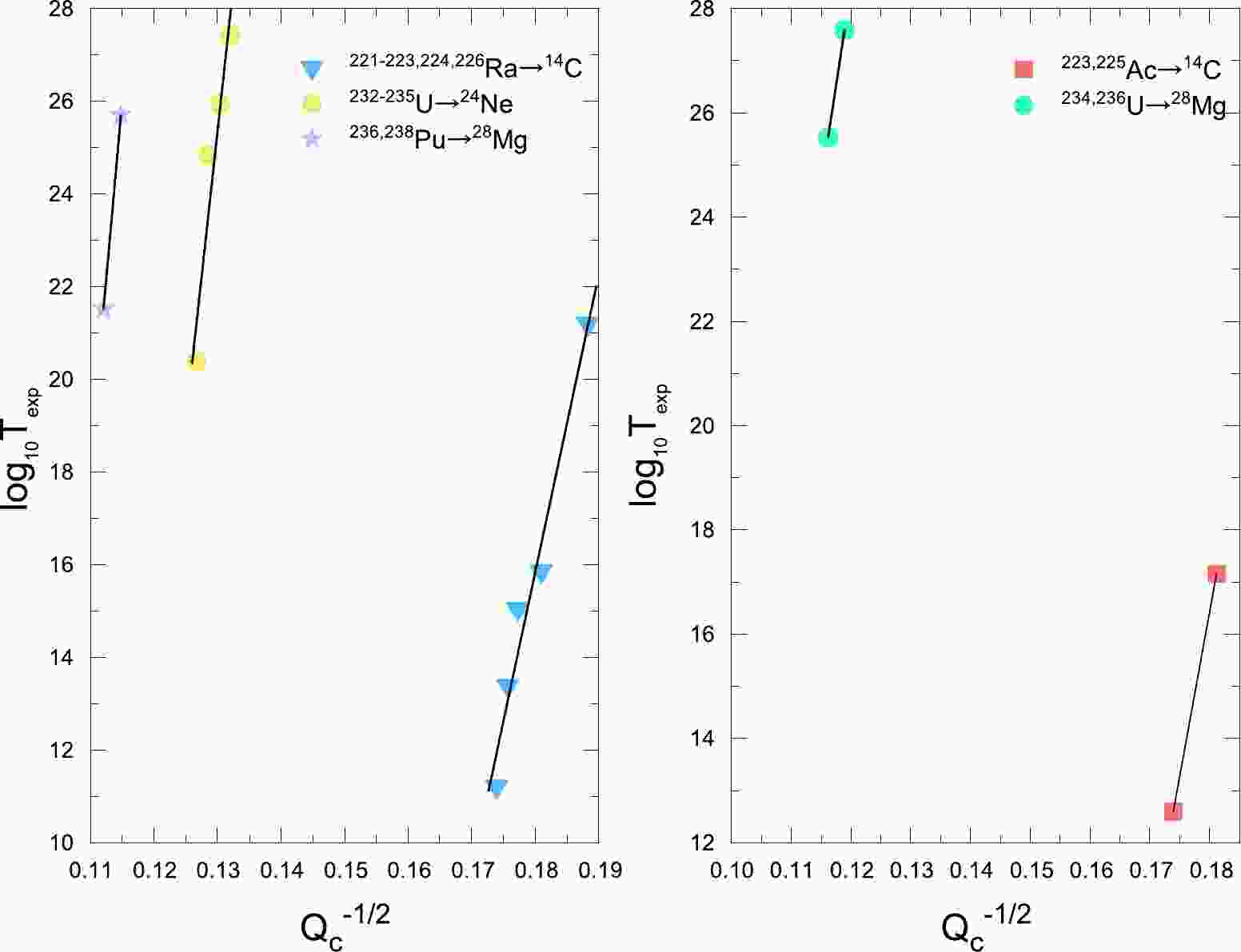
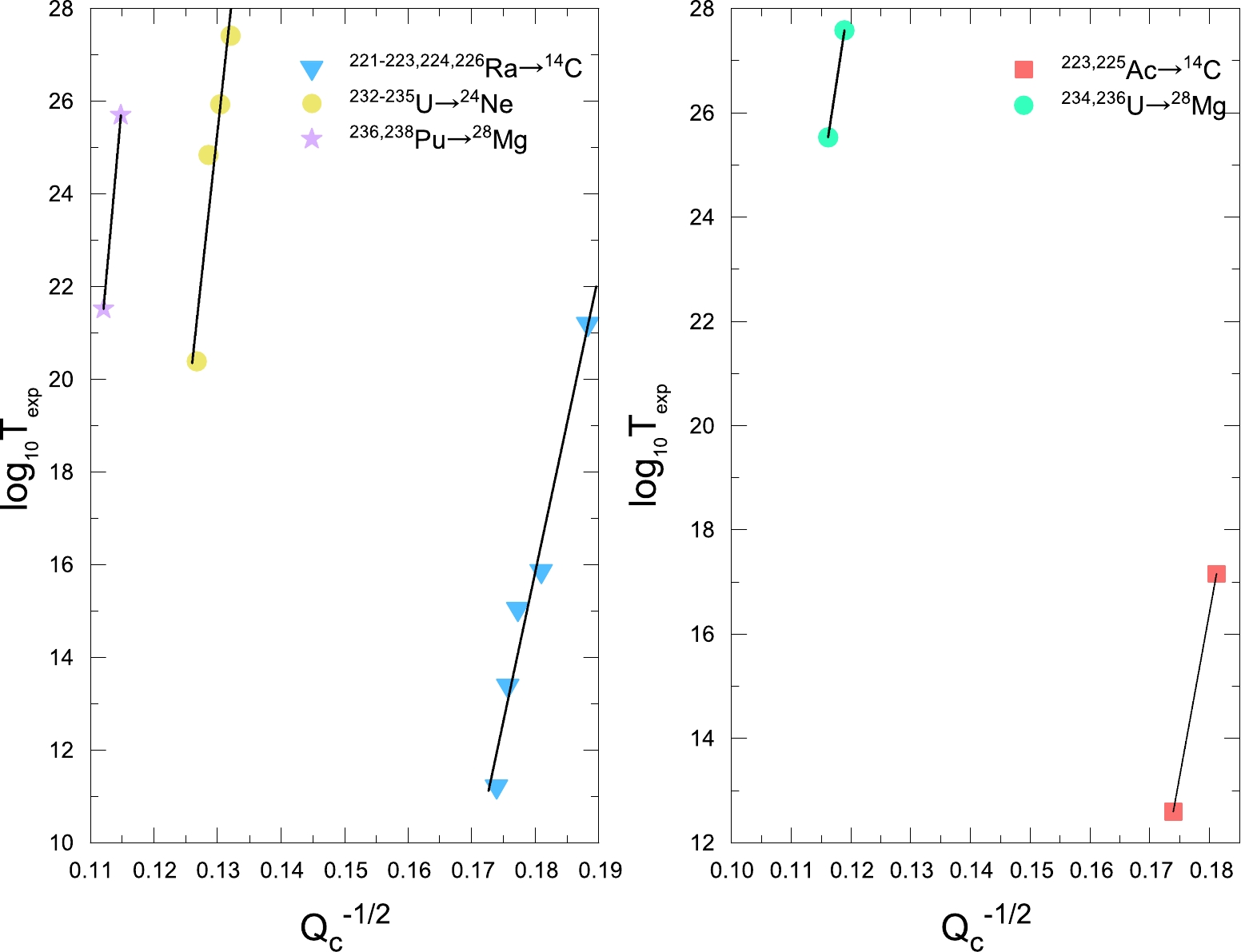
In this study, we propose a new G-N law to systematically study the cluster radioactivity half-lives of 26 nuclei. To intuitively validate the applicability of the G-N law to cluster radioactivity, the dependence between the experimental cluster radioactivity half-lives in logarithmic form and
$ Q_{c} ^{-1/2} $ for five cluster radioactive isotope cases is plotted in Fig. 1. The cluster radioactivity decay energy$ Q_{c} $ is calculated as below.$ Q_{c}=B(A_{c}, Z_{c})+B(A_{d}, Z_{d})-B(A, Z). $

(5) Here,
$ B(A_{c}, Z_{c}) $ ,$ B(A_{d}, Z_{d}) $ , and$ B(A, Z) $ are the binding energy of the emitted cluster, daughter, and parent nucleus, respectively. They are all taken from the latest 2020 atomic mass table AME2020 [51] and NUBASE2020 [52]. From Fig. 1, we can see that the experimental cluster radioactivity half-life in logarithmic form exhibits a linear relationship with$ Q_{c} ^{-1/2} $ for each case. Therefore, the construction of a semi-empirical formula for cluster radioactivity half-lives based on the G-N law is both physically reasonable and analytically numerical. Other than the cluster radioactive isotopes plotted above, there are still several individual cluster radioactivity cases with available experimental data that contribute to the study of cluster radioactivity, which should also be investigated. To break the isotopic dependent limit of the G-N law and further generalize it to all cluster radioactivity cases, it is necessary to probe more physical factors behind this phenomenon and make several advancements on the original G-N law.Experimentally, in the case of α decay, the reduced mass changes by 0.3% as the mass number of the daughter nucleus (
$ A_{d} $ ) changes from 200 to 300 [38]. It is rational to consider the reduced mass as a constant in the calculations of the half-lives of α decay. Nevertheless, the cluster radioactivity half-lives are extremely dependent on the reduced mass because its value promptly varies to both fragments of the emitted cluster and daughter nucleus [47]. In reality, for 14C radioactivity, the reduced mass changes by 0.15% as the mass number of the daughter nucleus ($ A_{d} $ ) changes from 207 to 212. As for 24Ne radioactivity, the reduced mass changes by 3.8% as the mass number of the daughter nucleus ($ A_{d} $ ) changes from 206 to 210. Moreover, Horoi also reported a proportional relationship between cluster radioactivity half-lives and the square root of the reduced mass$ \sqrt\mu $ [47]. Balasubramaniam's work has shown that cluster radioactivity half-lives in logarithmic form are dependent on both mass asymmetry η and charge asymmetry$ \eta_{z} $ [48]. Furthermore, the correlation between η and$ \eta_{z} $ is known to be weak, and they should be quantified separately [53, 54]. Therefore, it is interesting to explore whether the product of the square root of the reduced mass$ \sqrt\mu $ and mass asymmetry η as well as the product of the square root of the reduced mass$ \sqrt\mu $ and charge asymmetry$ \eta_{z} $ can be effectively supplemented into Balasubramaniam's original formula to improve the accuracy. For a distinct insight into the correlation between cluster radioactivity half-lives in logarithmic form and$ \sqrt{\mu}\eta $ and$ \sqrt{\mu}\eta_{z} $ , the correlations in the cases of 14C emitted from Ra isotopes and 24Ne emitted from U isotopes are plotted in Fig. 2 and Fig. 3, where the x axes represent$ \sqrt{\mu}\eta $ and/or$ \sqrt{\mu}\eta_{z} $ , respectively, and the y axes denote the cluster radioactivity half-lives in logarithmic form. From these two figures, it is clear that the cluster radioactivity half-lives in logarithmic form are linear to both$ \sqrt{\mu}\eta $ and$ \sqrt{\mu}\eta_{z} $ . Then, Balasubramaniam's formula can be revised as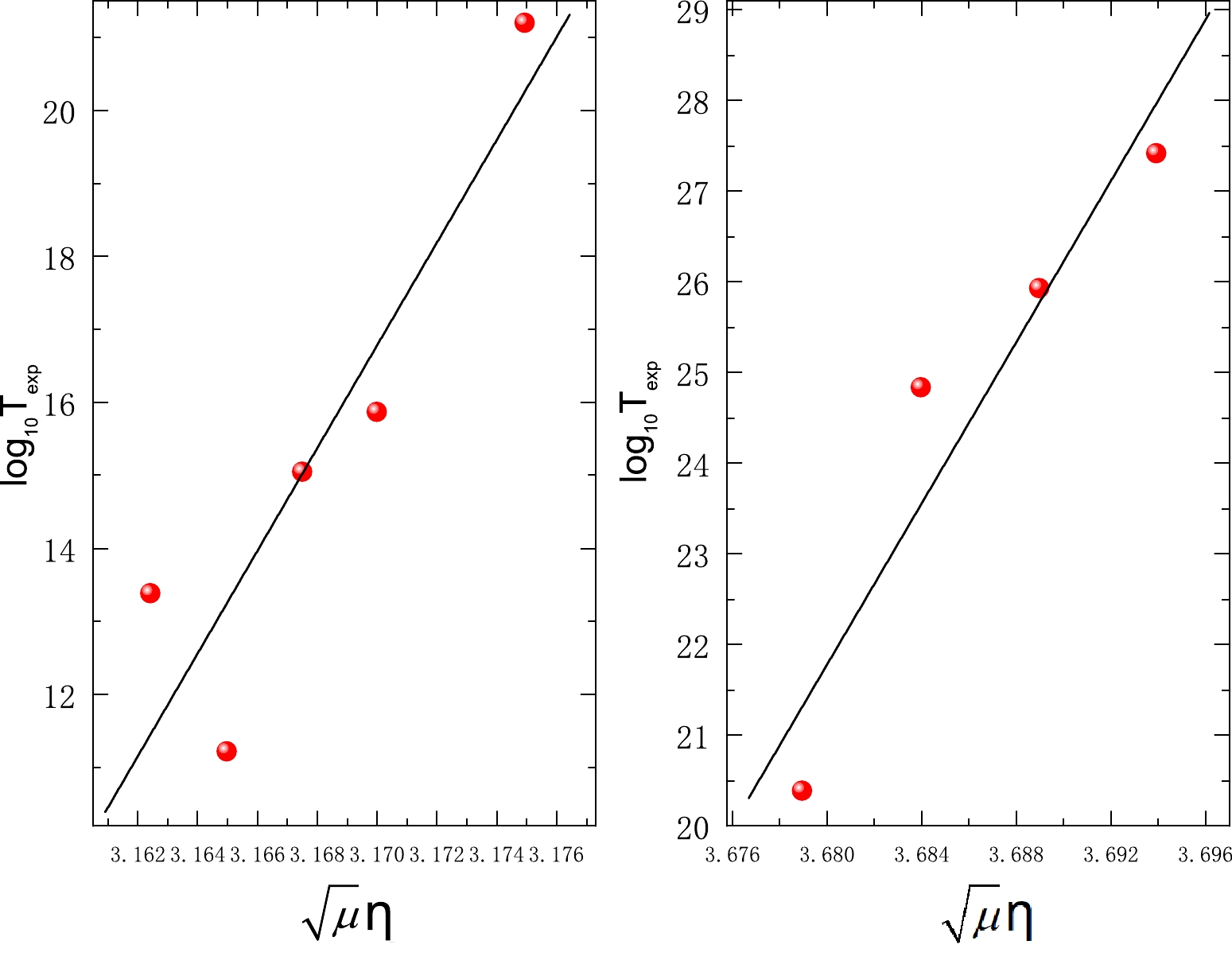
Figure 2. (color online) Correlation between the experimental cluster radioactivity half-lives in logarithmic form and
$\sqrt{\mu}\eta$ in the cases of 14C emitted from Ra isotopes and 24Ne emitted from U isotopes.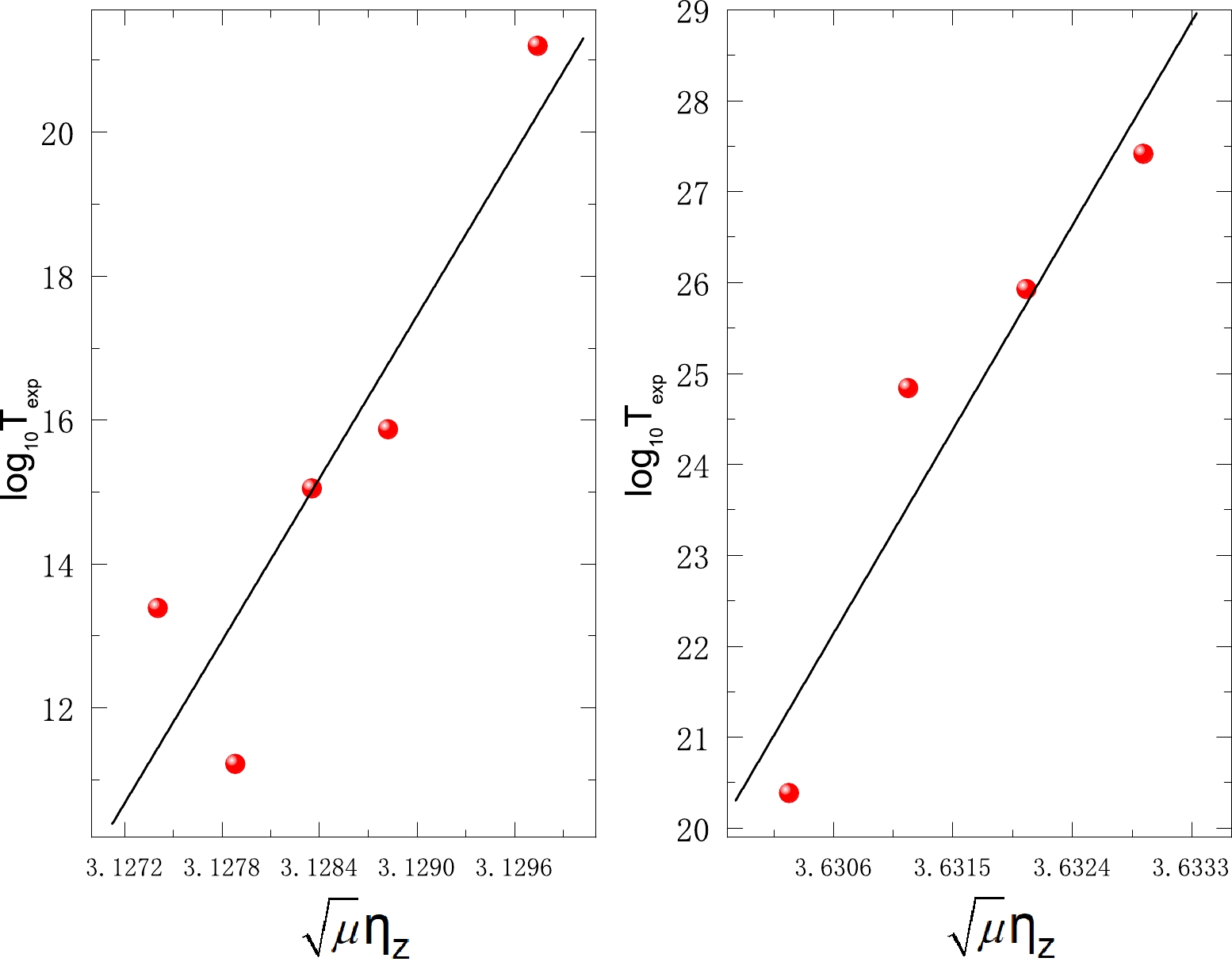
Figure 3. (color online) Correlation between the experimental cluster radioactivity half-lives in logarithmic form and
$\sqrt{\mu}\eta_{z}$ in the cases of 14C emitted from Ra isotopes and 24Ne emitted from U isotopes.$ \log_{10} (T_{1/2})=\frac{a_{1}A_{c}\eta+a_{2}Z_{c}\eta_{z}}{\sqrt{Q_{c}}}+\sqrt{\mu}(a_{3}\eta+a_{4}\eta_{z})+a_{5} . $

(6) Moreover, because the
$ a_{3}\sqrt{\mu}\eta $ and$ a_{4}\sqrt{\mu}\eta_{z} $ terms separately reflect the information of both η and$ \eta_{z} $ , to minimize the number of adjustable parameters, we make attempts to combine the first term$ a_{1}\dfrac{A_{c}\eta}{\sqrt{Q_{c}}} $ and second term$ a_{2}\dfrac{Z_{c}\eta_{z}}{\sqrt{Q_{c}}} $ as one term$ a_{1}\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}} $ . To justify the feasibility of this alteration, we plot the relationship between this term and the experimental half-lives of cluster radioactivity in logarithmic form in Fig. 4. This figure distinctly demonstrates that the experimental half-lives of cluster radioactivity in logarithmic form lie almost in a straight line against this combined term, as expected. Therefore, by further considering the blocking effect of odd-A nuclei characterized by the blocking factor h, Eq. 6 can be expressed as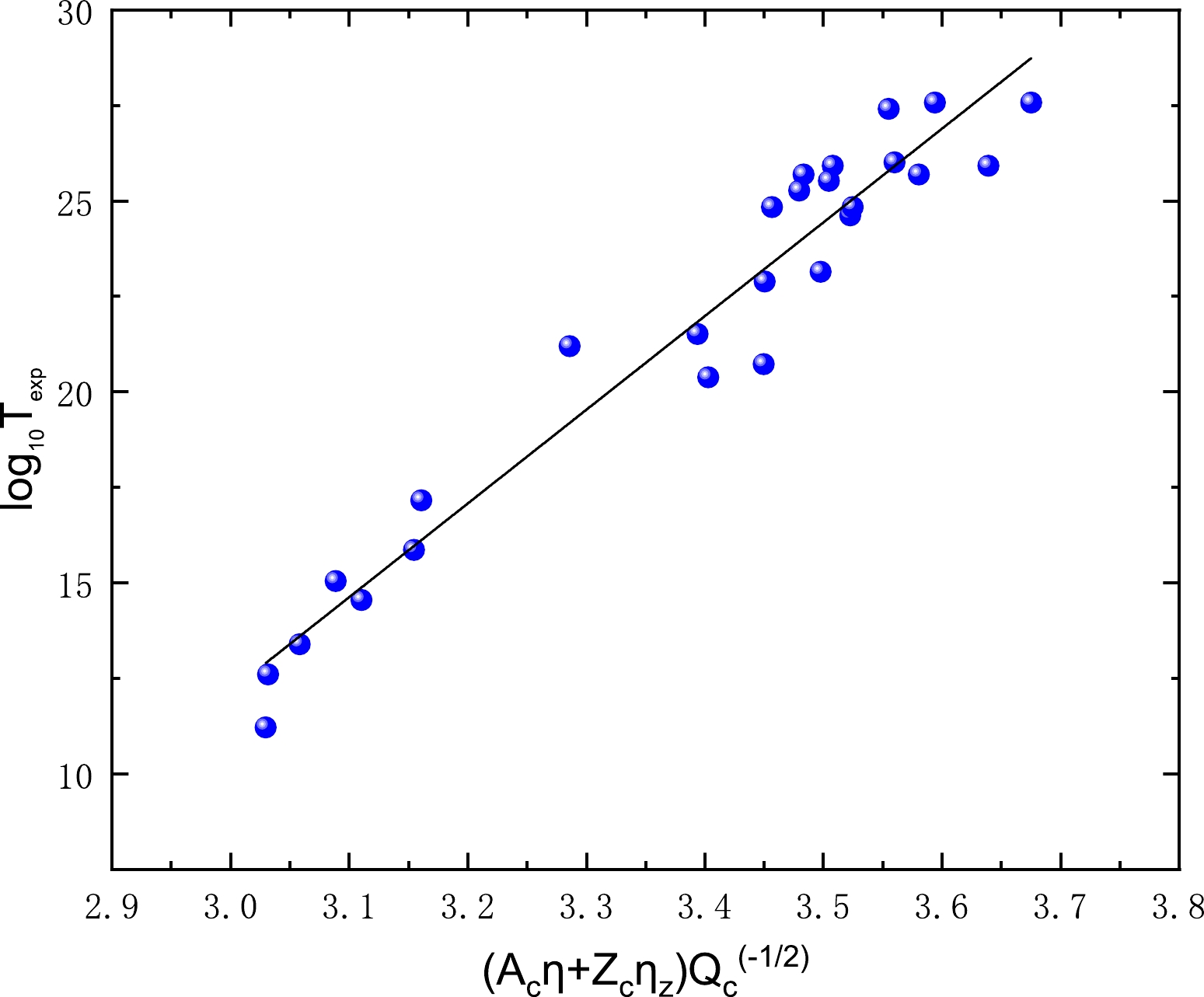
Figure 4. (color online) Correlation between the experimental cluster radioactivity half-lives in logarithmic form and the quantity
$\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}}$ .$ \log_{10} (T_{1/2})=a_{1}\frac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}}+\sqrt{\mu}(a_{2}\eta+a_{3}\eta_{z})+ a_{4}+h, $

(7) where
$ a_{1} $ ,$ a_{2} $ ,$ a_{3} $ , and$ a_{4} $ are the adjustable parameters, and σ represents the standard deviation between the experimental cluster radioactivity half-lives and the calculated values. In this study, it is defined as$ \sigma = \sqrt{\sum{({\rm log}_{10}{T_{1/2}^{{\rm exp}}}-{\rm log}_{10}{T_{1/2}^{{\rm cal}}})^2}/n}, $

(8) where
${\rm log}_{10}{T_{1/2}^{{\rm exp}}}$ and${\rm log}_{10}{T_{1/2}^{{\rm cal}}}$ are the experimental cluster radioactivity half-lives in logarithmic form and calculated values, respectively, and n is the number of nuclei involved for each case. Based on Eq. (7), the values of the adjustable parameters obtained using the least squares approach to fit the available experimental cluster radioactivity half-lives of 16 even-even emitters are$ a_{1} $ =31.081881,$ a_{2} $ =24.938505,$ a_{3} $ =−30.311899, and$ a_{4} $ =−66.443373.The blocking factor h=1.034577 is determined by fitting the experimental cluster radioactivity half-lives of 10 odd-A nuclei while
$ a_{1} $ ,$ a_{2} $ ,$ a_{3} $ , and$ a_{4} $ are fixed. To display the correlation between the quantity (${\rm log}_{10}{T_{1/2}^{{\rm exp}}}- \sqrt{\mu}(a_{2}\eta+a_{3}\eta_{z})-a_{4}-h_{\rm log}$ ) and the term$ a_{1}\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}} $ , we plot this correlation using the set of adjustable parameters between the quantity (${\rm log}_{10}{T_{1/2}^{{\rm exp}}}-\sqrt{\mu}(a_{2}\eta+a_{3}\eta_{z})- a_{4}-h_{\rm log}$ ) and the term$ a_{1}\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}} $ shown in Fig. 5. As clearly shown in this figure, there is a linear relationship between the experimental cluster radioactivity half-lives in logarithmic form and the results calculated using Eq. (7). The standard deviation between the experimental half-lives and calculated results for the 26 emitters is σ=0.739, which still implies large deviations between the experimental cluster radioactivity half-lives and calculated values.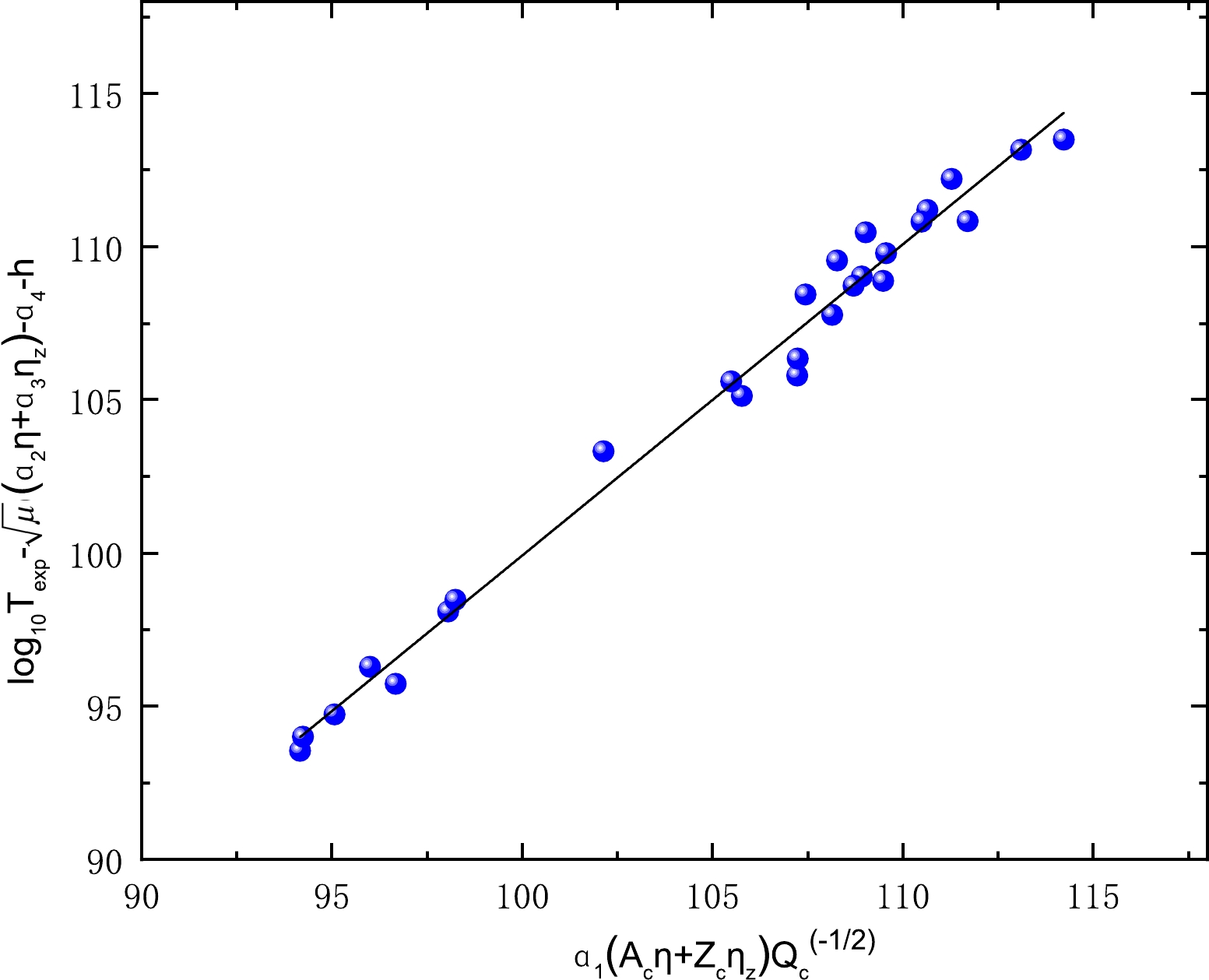
Figure 5. (color online) Linear correlation between the quantity [
${\rm log}_{10}{T_{1/2}^{{\rm exp}}}-\sqrt{\mu}(a_{2}\eta+a_{3}\eta_{z})-a_{4}-h$ ] and the term$a_{1}\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}}$ of Eq. (7).Previous phenomenological semi-empirical relationships concerning cluster radioactivity including Eq. (7) have placed considerable emphasis on the significance of the emitted cluster, which may impact the calculation of cluster radioactivity half-lives. In 2000, Royer indicated that the mass of the parent nucleus A is a key component in the calculation of α decay half-lives. With the similarity in the physical processes of α decay and cluster radioactivity, it is interesting to explore whether the mass of the parent nucleus A may also have an impact on cluster radioactivity half-lives. To this end, we plot the behavior of the experimental cluster radioactivity half-lives in logarithmic form against the mass of the parent nucleus A inFig. 6. Surprisingly, there is a visibly linear dependence between the experimental cluster radioactivity half-lives in logarithmic form and the mass of the parent nucleus A. The results illustrated in this figure verify the significance of probing the mass of the parent nucleus when estimating cluster radioactivity half-lives. Finally, based on Eq. (7), by further considering the effect of the parent nucleus mass A on cluster radioactivity half-life, we propose a new G-N law to evaluate cluster radioactivity half-lives, which can be expressed as
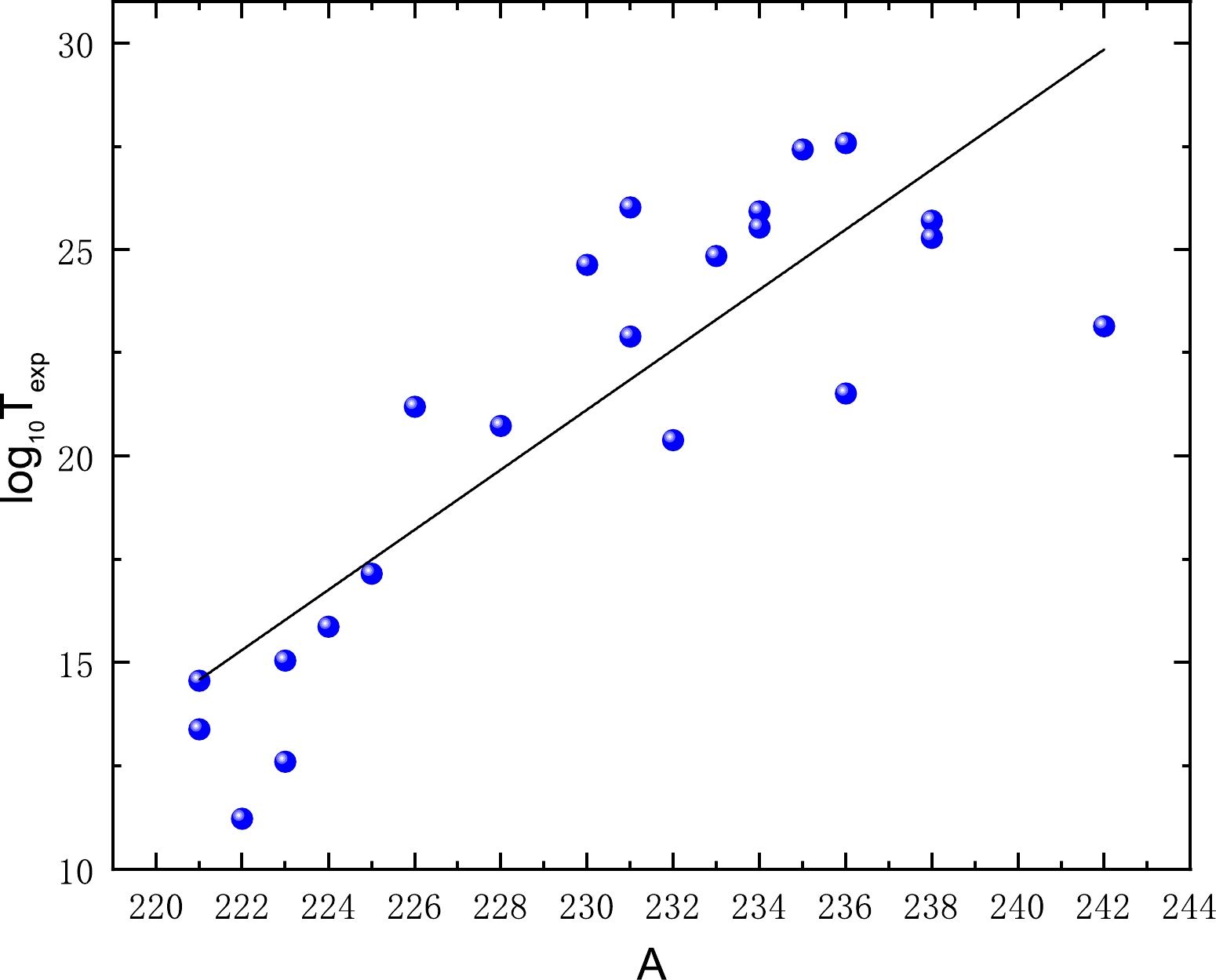
Figure 6. (color online) Correlation between the experimental cluster radioactivity half-lives in logarithmic form and the parent nucleus mass
$A$ .$ \log_{10} (T_{1/2})=a\frac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}}+\sqrt{\mu}(b\eta+c\eta_{z})+ dA+e+h_{\rm log}. $

(9) Here a, b, c, d, and e are the adjustable parameters, and
$h_{\rm log}$ is the blocking factor. By fitting the experimental half-lives of cluster radioactivity for the 16 even-even emitters while$h_{\rm log}$ =0, we obtain the values of these adjustable parameters as a=32.500137, b=18.117466, c=−29.999023, d=0.272744, and e=−111.134251.Moreover,
$h_{\rm log}$ =1.290933 is obtained by fitting the experimental half-lives of cluster radioactivity for 10 odd-A nuclei while a, b, c, d, and e are fixed. Using this set of parameters, the correlation between the quantity [${\rm log}_{10}{T_{1/2}^{{\rm exp}}} -\sqrt{\mu}(b\eta+c\eta_{z})-dA-e-h_{\rm log}$ ] and the term$ a\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}} $ is plotted in Fig. 7. From this figure, it is clear that the experimental cluster radioactivity half-lives in logarithmic form are proportional to the calculated results using our new G-N law. The standard deviation between the experimental half-lives and the calculated values obtained using Eq. (9) for the 26 emitters is 0.606. Compared to the calculated results obtained using Eq. (7), the standard deviation σ dramatically decreases by$ \dfrac{0.739-0.606}{0.739} $ =18.00%. Furthermore, the difference between the experimental half-lives and the calculated values using Eq. (7) and our new G-N law is plotted in Fig. 8. From this figure, we find that the distribution of the discrepancy of Eq. (7) is slightly scattered compared to that of the new G-N law, suggesting that the mass of the parent nucleus A is another important physical factor to be considered for cluster radioactivity half-lives, which may have been previously ignored.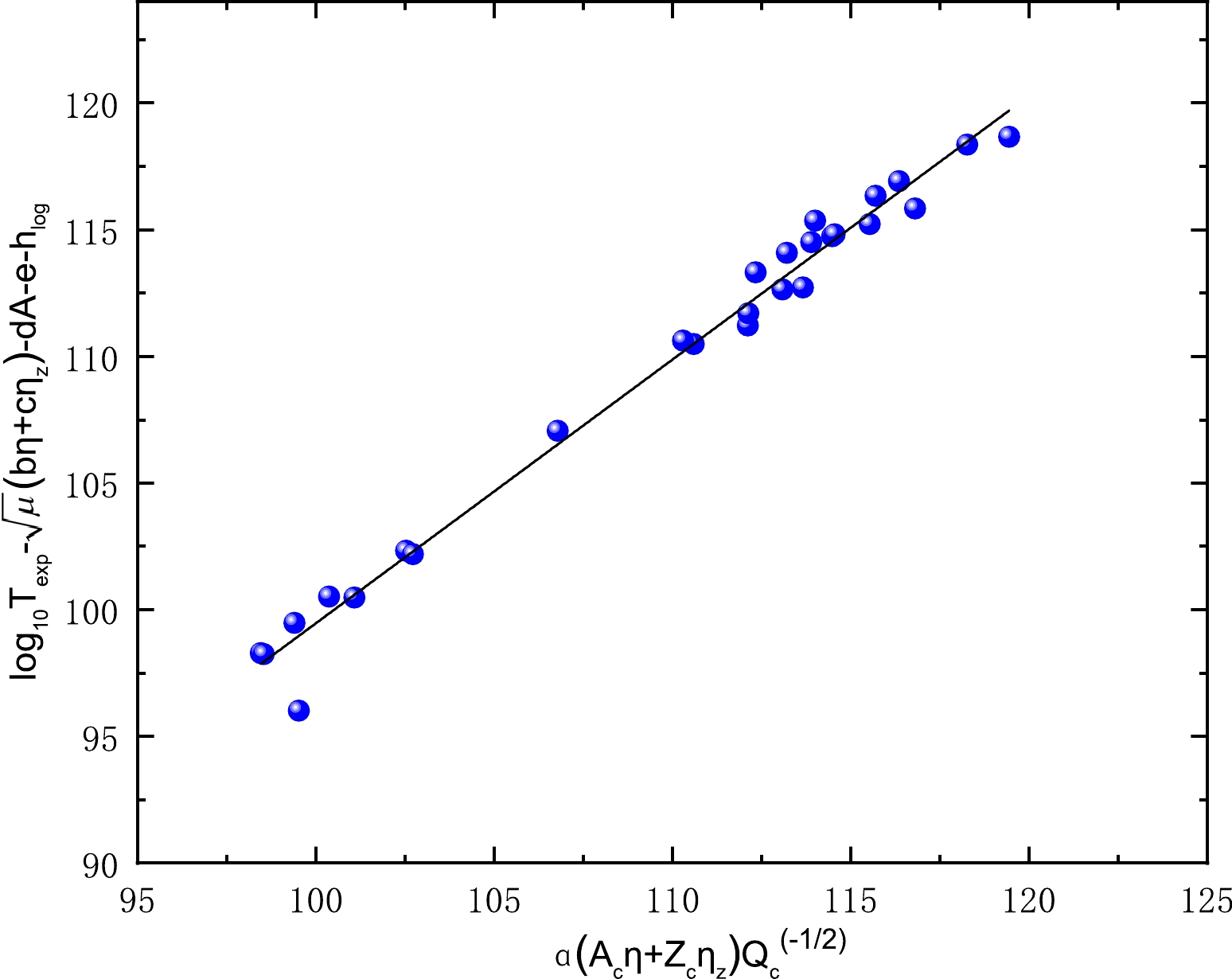
Figure 7. (color online) Linear correlation between the quantity [
${\rm log}_{10}{T_{1/2}^{{\rm exp}}} -\sqrt{\mu}(b\eta+c\eta_{z})-dA-e-h_{\rm log}$ ] and the term$a\dfrac{A_{c}\eta+Z_{c}\eta_{z}}{\sqrt{Q_{c}}}$ of Eq. (9).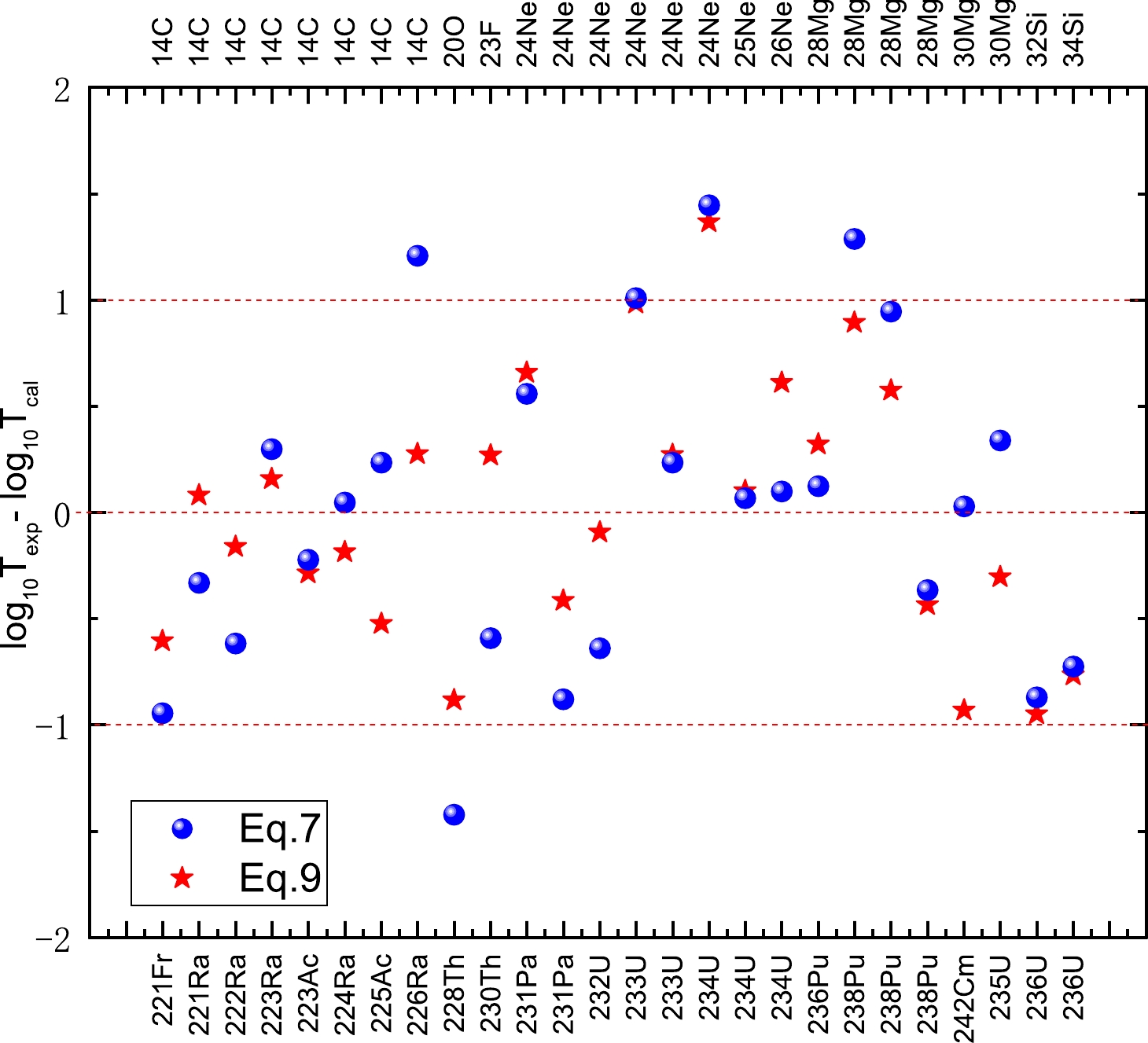
Figure 8. (color online) Differences between the experimental cluster radioactivity half-lives in logarithmic form and the calculated values obtained using Eqs. (7) and (9).
For comparison, the cluster radioactivity half-lives are also evaluated using UNIV [40], Ni's formula [38], EVS [37], the scaling law [47], and Balasubramaniam's formula [48]. The detailed calculated results are given in Table 1. In this table, the first two columns denote the decay process and cluster radioactivity decay energy, which are denoted as Decay and Q
$ _{c} $ , respectively. The experimental cluster radioactivity half-lives in logarithmic form extracted from Ref. [31], Ref. [44], and Ref. [55] are listed in the third column, denoted as$ \lg{T}_{1/2}^{\rm{exp}} $ . The fourth to tenth columns contain the calculated results obtained using UNIV, Ni's formula, the scaling law, Balasubramaniam's formula, EVS, Eq. (7), and our new G-N law, which are labeled as$ \lg{T}_{1/2}^{\rm{UNIV}} $ ,$ \lg{T}_{1/2}^{\rm{Ni}} $ ,$ \lg{T}_{1/2}^{\rm{SL}} $ ,$ \lg{T}_{1/2}^{\rm{Bala}} $ ,$ \lg{T}_{1/2}^{\rm{EVS}} $ ,$ \lg{T}_{1/2}^{\rm{Cal^{1}}} $ , and$ \lg{T}_{1/2}^{\rm{Cal^{2}}} $ , respectively. In this table, it is clear that the results calculated using EVS, Eq. (7), and our new G-N law are better than those calculated using UNIV, the scaling law, Balasubramaniam's formula, and Ni's formula.Decay ${Q}_{\rm c}/{\rm MeV}$ 

$\lg{T}_{1/2}^{\rm{exp}}$ 

$\lg{T}_{1/2}^{\rm{UNIV}}$ 

$\lg{T}_{1/2}^{\rm{Ni}}$ 

$\lg{T}_{1/2}^{\rm{SL}}$ 

$\lg{T}_{1/2}^{\rm{Bala}}$ 

$\lg{T}_{1/2}^{\rm{EVS}}$ 

$\lg{T}_{1/2}^{\rm{Cal^{1}}}$ 

$\lg{T}_{1/2}^{\rm{Cal^{2}}}$ 

221Fr→ 207Tl+14C 31.29 $^{+ 0.00707}_{-0.00707}$ 

14.56 14.22 14.63 13.54 14.65 14.43 15.51 15.17 $^{+ 0.01142}_{-0.01142}$ 

221Ra→207Pb+14C 32.40 $_{-0.00512}^{+0.00512}$ 

$ 13.39 $ 

$ 13.12 $ 

13.48 12.27 $ 13.14 $ 

$ 13.44 $ 

13.72 13.31 $^{+0.00786}_{-0.00785}$ 

222Ra→208Pb+14C 33.05 $_{-0.00415}^{+0.00415}$ 

11.22 11.95 11.02 11.00 12.23 10.74 11.84 11.38 $^{+0.00618}_{-0.00618}$ 

223Ra→209Pb+14C 31.83 $_{-0.00270}^{+0.00270}$ 

15.05 14.04 14.56 13.42 14.01 14.61 14.75 14.89 $^{+0.00426}_{-0.00426}$ 

224Ra→210Pb+14C 30.53 $_{-0.00228}^{+0.00228}$ 

15.87 16.42 15.86 16.14 16.01 15.98 15.82 16.06 $^{+0.00383}_{-0.00383}$ 

226Ra→ 212Pb+14C 28.20 $_{-0.00262}^{+0.00262}$ 

21.20 21.20 20.94 21.53 19.97 21.47 19.99 20.92 $^{+0.00496}_{-0.00496}$ 

223Ac→209Bi+14C 33.06 $_{-0.00714}^{+0.00714}$ 

12.60 12.73 13.19 11.93 12.35 13.37 12.82 12.89 $^{+0.01064}_{-0.01063}$ 

225Ac→211Bi+14C 30.48 $_{-0.00707}^{+0.00707}$ 

17.16 17.40 18.24 17.26 16.24 18.84 16.93 17.68 $^{+0.01192}_{-0.01191}$ 

228Th→208Pb+20O 44.72 $_{-0.00229}^{+0.00229}$ 

20.73 21.90 21.54 21.20 22.22 20.97 22.15 21.61 $^{+0.00287}_{-0.00287}$ 

231Pa→208Pb+23F 51.88 $_{-0.03007}^{+0.03007}$ 

26.02 24.47 25.59 23.78 24.65 24.62 25.46 25.36 $^{+0.03354}_{-0.03351}$ 

230Th→206Hg+24Ne 57.76 $_{-0.02004}^{+0.02004}$ 

24.63 24.68 24.58 23.92 25.68 24.17 25.22 24.36 $^{+0.01987}_{-0.01986}$ 

231Pa→207Tl+24Ne 60.41 $_{-0.00534}^{+0.00534}$ 

22.89 22.15 23.09 21.32 23.59 23.44 23.77 23.30 $^{+0.00495}_{-0.00495}$ 

232U→ 208Pb+24Ne 62.31 $_{-0.00217}^{+0.00217}$ 

20.39 20.76 20.36 19.94 22.26 21.00 21.03 20.48 $^{+0.00192}_{-0.00192}$ 

233U→ 209Pb+24Ne 60.49 $_{-0.00290}^{+0.00290}$ 

24.84 23.11 24.41 22.55 23.83 24.76 23.83 23.86 $^{+0.00270}_{-0.00270}$ 

234U→210Pb+24Ne 58.82 $_{-0.00185}^{+0.00185}$ 

25.93 25.38 25.81 25.03 25.32 25.61 24.48 24.56 $^{+0.00179}_{-0.00179}$ 

235U→211Pb+24Ne 57.36 $_{-0.00260}^{+0.00260}$ 

27.42 27.47 29.51 27.31 26.69 29.06 27.08 27.72 $^{+0.00262}_{-0.00262}$ 

233U→ 208Pb+25Ne 60.70 $_{-0.02911}^{+0.02911}$ 

24.84 23.75 24.88 23.05 24.43 24.48 24.61 24.57 $^{+0.02748}_{-0.02746}$ 

234U→208Pb+26Ne 59.41 $_{-0.01807}^{+0.01807}$ 

25.93 26.45 26.52 25.84 26.37 24.80 25.86 25.83 $^{+0.01799}_{-0.01798}$ 

234U→206Hg+28Mg 74.1 $_{-0.02003}^{+0.02003}$ 

25.53 25.19 25.25 24.76 25.95 25.11 25.43 24.92 $^{+0.01540}_{-0.01539}$ 

236U→208Hg+28Mg 70.73 $_{-0.03002 }^{+0.03002}$ 

27.58 29.37 30.33 29.28 28.54 29.11 28.45 28.53 $^{+0.02479}_{-0.02478}$ 

236Pu→208Pb+28Mg 79.67 $_{-0.00213}^{+0.00213}$ 

21.52 21.19 20.76 20.83 22.82 21.90 21.40 21.20 $^{+0.00147}_{-0.00147}$ 

238Pu→210Pb+28Mg 75.91 $_{-0.00180}^{+0.00180}$ 

25.70 25.35 25.96 25.42 25.42 26.00 24.41 24.81 $^{+0.00134}_{-0.00134}$ 

236U→206Hg+30Mg 72.27 $_{-0.02007}^{+0.02007}$ 

27.58 29.10 29.47 28.69 28.64 27.25 28.31 28.35 $^{+0.01659}_{-0.01658}$ 

238Pu→208Pb+30Mg 76.80 $_{-0.00203}^{+0.00203}$ 

25.70 25.97 26.10 25.71 26.05 25.01 24.76 25.13 $^{+0.00154}_{-0.00154}$ 

238Pu→206Hg+32Si 91.19 $_{-0.02003}^{+0.02003}$ 

25.28 25.50 25.59 25.70 25.63 25.34 25.65 25.71 $^{+0.01242}_{-0.01242}$ 

242Cm →208Pb+34Si 96.51 $_{-0.00175}^{+0.00175}$ 

23.15 23.91 23.48 24.21 24.46 23.16 23.12 24.08 $^{+0.00103}_{-0.00103}$ 

Table 1. Comparisons between the experimental cluster radioactivity half-lives (in seconds) in logarithmic form and the calculated values using different formulas.
Furthermore, the calculated results of σ using UNIV, Ni's formula, the scaling law, EVS, Balasubramaniam's formula, Eq. (7), and our new G-N law are also provided in Table 2. From this table, it is clear that for even-even nuclei, the values of σ obtained using EVS and our new G-N law are essentially consistent and smaller than those calculated using UNIV, Ni's formula, the scaling law, Balasubramaniam's formula, and Eq. (7). For odd-A nuclei, the value of σ calculated using our new G-N law is
$ \sigma=0.499 $ , which is the smallest out of all the results. Moreover, for all 26 nuclei, the value of σ calculated using our new G-N law is$ \sigma=0.606 $ , corresponding to a factor of 4 on average, which is comparably less than the results of all compared formulas. By comparing the results of EVS, which are the closest to our results from the new G-N law, the standard deviation of the half-lives for 26 nuclei decreases by$\dfrac{0.744-0.606}{0.744}$ =18.55%. Compared to the results from Balasubramaniam's original version, our new G-N law improves by$\dfrac{0.921-0.606}{0.921}$ =34.20%. This means that the results calculated using our new G-N law are in good agreement with the experimental cluster radioactivity half-lives. It should be noted that the differences in physical object selection and the corresponding construction conception using different numbers of parameters for different analytical formulas cause the differences in rms deviation.σ UNIV Ni SL Bala EVS Cal1 Cal2 even-even (n=16) 0.769 0.913 0.731 0.997 0.595 0.819 0.662 odd-A (n=10) 0.918 0.808 1.462 0.784 0.935 0.590 0.499 total (n=26) 0.829 0.874 1.073 0.921 0.744 0.738 0.606 Table 2. Standard deviation σ between the experimental data and the calculated values using different formulas for cluster radioactivity.
To make further intuitive comparisons, we plot the discrepancies between the experimental cluster radioactivity half-lives in logarithmic form and the calculated values obtained using UNIV, Ni's formula, the scaling law, EVS, Balasubramaniam's formula, Eq. (7), and our new G-N law in Fig. 9. In this figure, the discrepancies are depicted in two parts: comparisons to model-dependent formulas (UNIV, Ni's formula, and EVS) and model-independent formulas (scaling law and Balasubramaniam's formula). We can distinctly see that compared with the model-dependent formulas, the distributions of the discrepancies for EVS, Eq. (7), and our new G-N law are more converging on the zero area based on the overall trend. The calculated results of our new G-N law are within ±1 overall, except for the case of 234U→210Pb+24Ne, which has a discrepancy of 1.37, perhaps owing to the imprecision of measurement. For the calculated results of EVS and Eq. (7), both have five cases whose discrepancies are outside the scale of ±1 for all 26 nuclei. For the discrepancies of UNIV, there are nine cases beyond of the scale of ±1. For the calculated results of Ni's formula, the case of 235U→211Pb+24Ne, which has a discrepancy of 2.089, and the case of 236Pu→208Pb+28Mg, which exhibits a discrepancy of 2.748, are outside the scale of ±2. For the comparisons with model-independent formulas, the discrepancies of Balasubramaniam's formula are within ±2 overall, with 11 nuclei whose discrepancies are beyond of the scale of ±1. For the scaling law, there are 10 nuclei whose discrepancies are beyond of the scale of ±1, with a discrepancy of 2.242 in the case of 231Pa→208Pb+23F and a discrepancy of 2.290 in the case of 233U→ 209Pb+24Ne. The results demonstrated in Fig. 9 further show that our new G-N law can reproduce the experimental cluster radioactivity half-lives well.
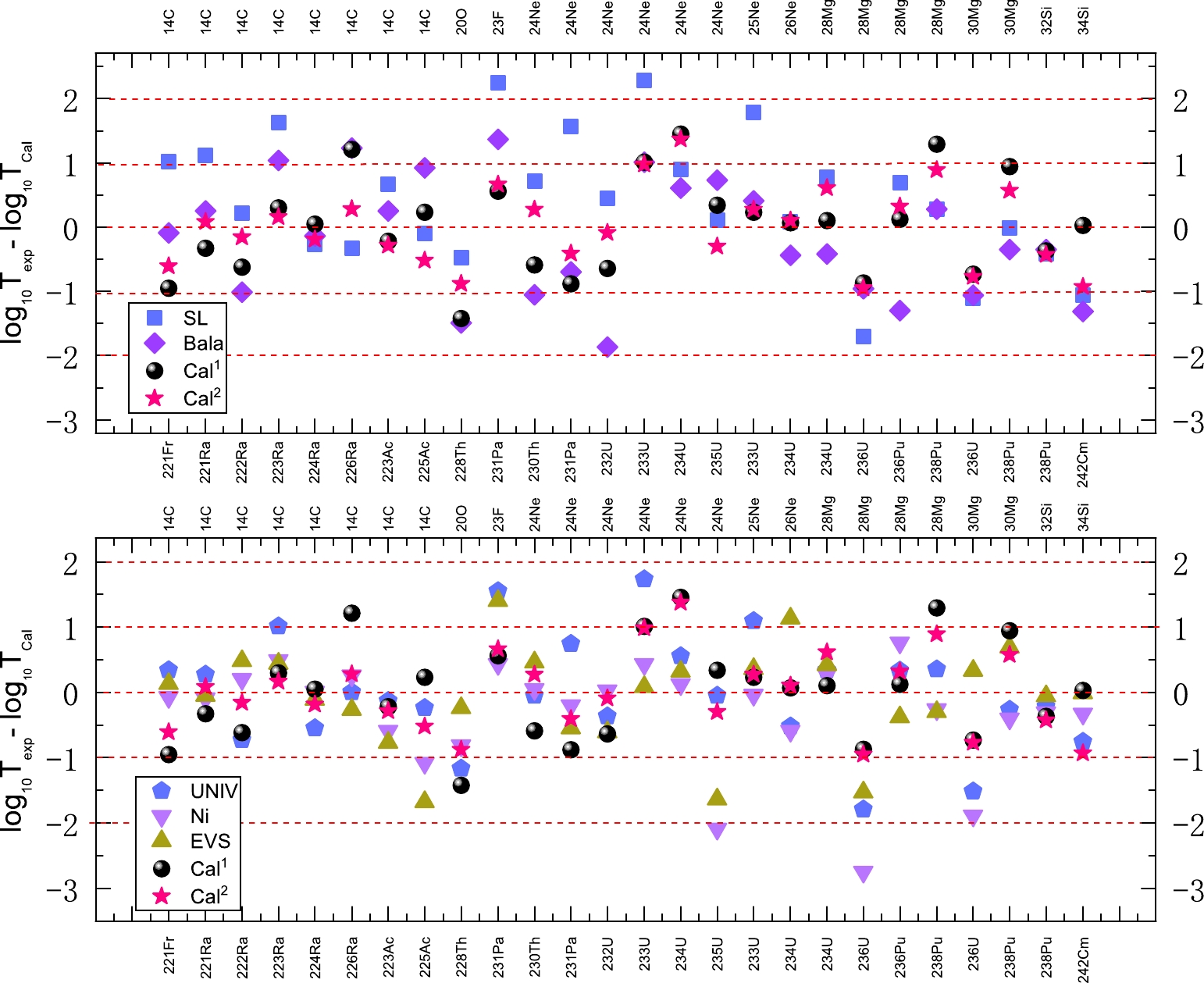
Figure 9. (color online) Comparison of the discrepancies between the experimental cluster radioactivity half-lives in logarithmic form and the calculated values obtained using different semi-empirical formulas and our new G-N law. The top diagram presents the comparison with the calculated results obtained using the model-independent semi-empirical formulas of the scaling law and Balasubramaniam's formula. The bottom diagram presents the comparison with the calculated results obtained using the model-dependent semi-empirical formulas of UNIV, Ni’s formula, and EVS.
Furthermore, the cluster radioactivity half-lives are extremely sensitive to
$ Q_{c} $ values. A change of 1 MeV in$ Q_{c} $ can lead to an uncertainty ranging from 102 to 103 times on the cluster radioactivity half-life [56]. Because the experimental values of binding energies have uncertainties, the theoretical values of$ Q_{c} $ and cluster radioactivity half-lives also have uncertainties. However, the uncertainties of$ Q_{c} $ cannot be directly experimentally measured. The uncertainties of$ Q_{c} $ can possibly be evaluated through the error propagation formula. If there is a linear correlation between the physical quantity whose uncertainty needs to be estimated and other quantities whose uncertainties have been experimentally measured,$ y= a_{0}+a_{x_{1}}x_{1}+a_{x_{2}}x_{2}+a_{x_{3}}x_{3}, $

(10) where
$ a_{x_{1}} $ ,$ a_{x_{2}} $ , and$ a_{x_{3}} $ are the coefficients of$ x_{1} $ ,$ x_{2} $ , and$ x_{3} $ , respectively, and$ a_{0} $ is simply a constant. The uncertainties of the physical quantity can be indirectly calculated using the following formula:$ \begin{aligned}[b] \sigma^{2} =& a_{x_{1}}^{2}\sigma^{2}_{x_{1}}+a_{x_{2}}^{2}\sigma^{2}_{x_{2}}+a_{x_{3}}^{2}\sigma^{2}_{x_{3}}+2a_{x_{1}}a_{x_{2}}{\rm Cov}(x_{1}, x_{2})\\&+2a_{x_{1}}a_{x_{3}} {\rm Cov} (x_{1}, x_{3})+2a_{x_{2}}a_{x_{3}} {\rm Cov}(x_{2}, x_{3}), \end{aligned} $

(11) where
$ \sigma_{x_{1}} $ ,$ \sigma_{x_{2}} $ , and$ \sigma_{x_{3}} $ are the uncertainties of$ x_{1} $ ,$ x_{2} $ , and$ x_{3} $ , respectively, and${\rm Cov}(x_{1}, x_{2})$ ,${\rm Cov}(x_{1}, x_{3})$ , and${\rm Cov}(x_{2}, x_{3})$ denote the covariance between$ x_{1} $ and$ x_{2} $ , the covariance between$ x_{1} $ and$ x_{3} $ , and the covariance between$ x_{2} $ and$ x_{3} $ , respectively. If the variables$ x_{1} $ ,$ x_{2} $ , and$ x_{3} $ are independent, Eq. (11) can be simplified as$ \sigma^{2} = a_{x_{1}}^{2}\sigma^{2}_{x_{1}}+a_{x_{2}}^{2}\sigma^{2}_{x_{2}}++a_{x_{3}}^{2}\sigma^{2}_{x_{3}}. $

(12) In the case of cluster radioactivity, the uncertainties of
$ Q_{c} $ can be obtained using$ \Delta Q_{c}= \sqrt{\Delta^{2} B(A_{c}, Z_{c})+\Delta^{2}B(A_{d}, Z_{d})+\Delta^{2} B(A, Z)}, $

(13) where
$ \Delta B(A_{c}, Z_{c}) $ ,$ \Delta B(A_{d}, Z_{d}) $ , and$ \Delta B(A, Z) $ represent the experimental uncertainties of$ B(A_{c}, Z_{c}) $ ,$ B(A_{d}, Z_{d}) $ , and$ B(A, Z) $ extracted from NUBASE2020 [52]. The relative sizes of the uncertainties of both the$ Q_{c} $ values and corresponding theoretical cluster radioactivity half-lives are also provided in Table 1. The good agreement between the experimental half-lives and the calculated values using our new G-N law presented in Table 1, Table 2, and Fig. 9 confirms that the new G-N law is reliable for cluster radioactivity half-life calculations. Therefore, we extend our new G-N law to predict the half-lives of 51 possible cluster radioactivity candidates, and the calculated results are displayed in Table 3. In this table, the labels of the first to eighth columns are similar to those of Table 1, except for the ninth column, which represents the predicted results of our new G-N law, denoted as$ \lg{T}_{1/2}^{\rm{Cal}} $ . From Table 3, it is clear that the predicted results of our new G-N law are essentially consistent with the predicted values obtained using the compared formulas. In this table, we easily notice that in the case of 233U→ 205Hg+28Mg, the theoretical predicted half-lives calculated using all the analytical formulas are lower than the experimental bound by one to three orders of magnitude. A possible physical reason behind this result may be the effect of the proton subshell Z=92. Previous studies have discovered that the preformation probability near proton and neutron subshells strangely increase owing to the enhanced proton-neutron interactions, which results in a shorter half-life [57, 58]. This further confirms that cluster radioactivity is closely related to the nuclear structure. We hope that this study can be an effective tool toward theoretical investigation of cluster radioactivity and further provide a theoretical guide for future experiments.Decay $Q_{c}/{\rm MeV}$ 

$\lg{T}_{1/2}^{\rm{exp}}$ 

$\lg{T}_{1/2}^{\rm{UNIV}}$ 

$\lg{T}_{1/2}^{\rm{Ni}}$ 

$\lg{T}_{1/2}^{\rm{SL}}$ 

$\lg{T}_{1/2}^{\rm{Bala}}$ 

$\lg{T}_{1/2}^{\rm{EVS}}$ 

$\lg{T}_{1/2}^{\rm{Cal}}$ 

219Rn→ 205Hg+14C 28.10 − 19.77 20.29 19.65 19.75 20.33 20.16 220Rn→ 206Hg+14C 28.54 − 18.78 18.05 18.61 18.99 17.86 18.40 221Fr→ 206Hg+15N 34.12 − 21.23 22.16 20.81 21.32 24.12 19.67 223Ra→ 205Hg+18O 40.30 − 25.27 26.41 24.74 24.99 27.35 23.72 225Ra→ 211Pb+14C 29.47 − 18.51 19.37 18.53 17.76 19.81 19.54 225Ra→ 205Hg+20O 40.48 − 27.31 28.34 26.86 27.00 27.01 27.77 226Ra→ 206Hg+20O 40.82 − 26.62 26.41 26.18 26.59 24.98 26.40 223Ac→ 208Pb+15N 39.47 >14.76 13.84 14.47 12.90 14.50 16.53 12.74 227Ac→ 207Tl+20O 43.09 − 23.61 24.55 22.99 23.94 23.75 24.79 229Ac→ 206Hg+23F 48.35 − 27.91 29.14 27.30 27.93 27.24 29.08 226Th→ 208Pb+18O 45.73 >16.76 18.20 17.81 17.38 18.96 19.32 16.45 226Th→ 212Po+14C 30.55 >15.36 18.13 17.83 18.10 16.27 18.61 16.51 227Th→ 209Pb+18O 44.20 − 20.54 21.69 19.96 20.68 23.25 19.91 228Th→ 206Hg+22Ne 55.74 − 25.73 26.07 25.14 25.83 27.03 23.36 229Th→ 209Pb+20O 43.40 − 24.08 25.25 23.64 23.80 24.62 24.99 229Th→ 205Hg+24Ne 57.83 − 24.65 25.72 23.80 25.59 25.48 25.16 231Th→ 207Hg+24Ne 56.25 − 26.85 28.36 26.29 27.12 27.69 27.61 231Th→ 206Hg+25Ne 56.80 − 27.02 28.30 26.31 27.42 26.92 28.04 232Th→ 208Hg+24Ne 54.67 >29.2 29.26 29.86 28.89 28.71 28.62 28.42 232Th→ 206Hg+26Ne 55.91 >29.2 29.31 29.45 28.66 29.10 26.79 29.06 227Pa→ 209Bi+18O 45.87 − 18.96 20.01 18.27 19.00 21.86 17.79 229Pa→ 207Tl+22Ne 58.96 − 22.31 23.63 21.67 23.16 25.38 21.76 230U→ 208Pb+22Ne 61.39 >18.2 20.20 20.09 19.55 21.35 22.18 18.49 230U→ 206Pb+24Ne 61.35 >18.2 22.14 21.78 21.27 23.00 22.23 20.49 232U→ 204Hg+28Mg 74.32 >22.26 25.08 24.93 24.47 25.73 24.88 23.84 233U→ 205Hg+28Mg 74.23 >27.59 25.12 26.33 24.60 25.84 26.38 25.66 235U→ 211Pb+24Ne 57.36 >27.65 27.47 29.51 27.31 26.69 29.06 27.72 235U→ 210Pb+25Ne 57.68 >27.65 27.99 29.86 27.72 27.21 28.61 28.40 235U→ 207Hg+28Mg 72.43 >28.45 27.22 29.00 26.98 27.22 28.47 27.99 235U→ 206Hg+29Mg 72.48 >28.45 28.03 29.67 27.66 27.83 28.41 28.50 236U→ 212Pb+24Ne 55.95 >26.27 29.61 30.71 29.60 28.07 29.73 28.31 236U→ 210Pb+26Ne 56.69 >26.27 30.48 31.23 30.27 28.98 28.63 29.53 236U→ 208Hg+28Mg 70.73 >26.27 29.37 30.33 29.28 28.54 29.11 28.53 236U→ 206Hg+30Mg 72.27 >26.27 29.10 29.47 28.69 28.64 27.25 28.35 238U→ 208Hg+30Mg 69.46 − 32.81 33.98 32.72 30.91 30.69 31.71 231Np→ 209Bi+22Ne 61.90 − 20.61 21.95 20.10 21.18 24.32 19.53 233Np→ 209Bi+24Ne 62.16 − 22.05 23.24 21.46 22.64 23.98 22.10 235Np→ 207Tl+28Mg 77.10 − 22.88 23.92 22.48 24.20 24.64 24.15 237Np→ 207Tl+30Mg 74.79 >27.57 27.17 28.63 26.82 27.13 27.22 27.79 237Pu→ 209Pb+28Mg 77.73 − 23.29 24.66 23.16 24.14 25.38 24.32 237Pu→ 208Pb+29Mg 77.45 − 24.43 25.73 24.18 24.95 25.68 25.01 237Pu→ 205Hg+32Si 91.46 − 25.29 26.48 25.39 25.43 26.47 26.35 239Pu→ 209Pb+30Mg 75.08 − 28.01 29.89 27.95 27.29 28.34 28.21 239Pu→ 205Hg+34Si 90.87 − 27.29 28.50 27.29 26.85 27.05 28.05 237Am→ 209Bi+28Mg 79.85 − 22.15 23.35 22.02 23.02 24.52 22.54 239Am→ 207Tl+32Si 94.50 − 23.38 24.38 23.66 24.14 25.03 25.14 241Am→ 207Tl+34Si 93.96 >24.41 25.26 26.26 25.44 25.51 25.54 26.77 240Cm→ 208Pb+32Si 97.55 − 21.64 21.09 22.02 22.87 22.24 22.24 241Cm→ 209Pb+32Si 95.39 − 23.66 25.02 24.26 24.07 25.63 25.25 243Cm→ 209Pb+34Si 94.79 − 25.61 27.00 26.12 25.47 26.19 26.92 244Cm→ 210Pb+34Si 93.17 − 27.24 27.89 27.92 26.43 26.34 27.12 Table 3. Predicted half-lives for possible cluster radioactive nuclei.
-
In summary, based on Balasubramaniam's formula and considering the effect of the parent nucleus mass, blocking effect of unpaired nucleons, and reduced mass on cluster radioactivity half-lives, we propose a new G-N law for cluster radioactivity. The calculated cluster radioactivity half-lives obtained using our new G-N law are found to be in better agreement with experimental data with a least rms deviation of 0.606 compared with the results obtained using UNIV, the scaling law, EVS, Balasubramaniam's formula, and Ni's formula. The corresponding rms deviations are 0.829, 1.073, 0.744, 0.921, and 0.874, respectively. Furthermore, we extend our new G-N law to predict the cluster radioactivity half-lives of 51 nuclei whose decay energy are energetically allowed or observed but not yet quantified, and the decay energy
$ Q_{c} $ is calculated from the latest 2020 atomic mass table. The predictions of our new G-N law are essentially consistent with those obtained using UNIV, the scaling law, EVS, Balasubramaniam's formula, and Ni's formula. The results of this study may be useful for probing the nuclear structure in future experiments.
New Geiger-Nuttall law for cluster radioactivity half-lives
- Received Date: 2023-01-18
- Available Online: 2023-06-15
Abstract: In this study, derived from Balasubramaniam's formula [Phys. Rev. C 70, 017301 (2004)] and further considering the effect of the parent nucleus mass, blocking effect, and effect of reduced mass on cluster radioactivity half-lives, we propose a new Geiger-Nuttall law that is model-independent to systematically evaluate the half-lives of this process for 16 even-even nuclei and 10 odd-A nuclei. For comparison, a single universal curve for cluster radioactivity and α decay proposed by Poenaru [Phys. Rev. C 83, 014601 (2011)], a scaling law proposed by Horoi [J. Phys. G: Nucl. Part. Phys. 30, 945 (2004)], an extension of the Viola-Seaborg formula from α decay to cluster radioactivity proposed by Ren et al. [Phys. Rev. C 70, 034304 (2004)], a new semi-empirical formula for exotic cluster decay proposed by Balasubramaniam et al. [Phys. Rev. C 70, 017301 (2004)], and a unified formula for the half-lives of α decay and cluster radioactivity proposed by Ni et al. [Phys. Rev. C 78, 044310 (2008)] are also used. The calculated results of our new Geiger-Nuttall law are in good agreement with the experimental half-lives, with the least rms being 0.606, and are better than the compared values. Moreover, we extend this formula to predict the cluster radioactivity half-lives of 51 nuclei whose decay energies are energetically allowed or observed but not yet quantified in NUBASE2020.


 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: