-
Vector mesons in low energy photoproduction play an essential role in understanding the vector meson-proton (V-p) interaction [1]. The most apparent manifestation is the scattering length of the V-p interaction. Researchers now calculate the scattering length of the V-p interaction by establishing theoretical models or analyzing experimental data, such as ρ-p, ω-p, ϕ-p,
$ J/\psi $ -p,$ \psi(2S) $ -p, and Υ-p [1–10]. As a conventional$ s\bar{s} $ state, ϕ has been extensively investigated. To study the internal structure of a proton, some researchers extract the mass radius of the proton from the cross section of ϕ photoproduction at the near-threshold [11, 12]. Others have moved on to the scattering length of the ϕ-p interaction. The earliest study can be traced back to 1997, when Koike et al. [4] used QCD sum rules to analyze the scattering length of spin-isospin average ρ-p, ω-p, and ϕ-p. Via the low energy limit constraint of the forward scattering amplitude of the vector-current nucleon,$ \alpha_{\rho p}=-0.47\pm0.05 $ fm,$\alpha_{\omega p}=-0.41\pm 0.05$ fm, and$ \alpha_{\phi p}=-0.15\pm0.02 $ fm were obtained. In 2000, Gao et al. [13] analyzed the ϕ-N bound state through the QCD van der Waals attractive potential and believed that the ϕ-N bound state can help detect the strangeness content of nucleons. In 2007, the LEPS Collaboration [3] obtained$ \alpha_{\phi p}=-0.15 $ fm from the differential experimental cross sections of$ \gamma p $ $ \rightarrow $ $ \phi p $ at the near-threshold for the first time. In the same period, Titov et al. [1] related the differential cross section of ϕ photoproduction to scattering length by establishing the vector meson dominant (VMD) model. This indicates that the differential cross section of ϕ at the threshold is finite, and its behavior is crucial for the QCD-inspired ϕ-p interaction model. The study of the scattering length of the ϕ-p interaction then fell silent.In recent years, the investigation of the scattering length of the V-p interaction has been revived owing to the accumulation of experimental data on vector meson photoproduction. In 2014, Strakovsky et al. [7] used odd power polynomials to fit the total experimental cross section of ω photoproduction and obtained
$ |\alpha_{\omega p}|=0.81\pm 0.41 $ fm. In 2020, they [2, 10] combined the total experiment cross section of vector meson photoproduction with the VMD model.$ |\alpha_{J/\psi p}| =3.08 \pm 0.55 $ am and$ |\alpha_{\phi p}| =0.063\pm 0.01 $ fm were obtained by fitting the odd power polynomials with the latest photoproduction data. Subsequently, the same researchers [9] combined the differential cross section of$ J/\psi $ photoproduction with the scattering length based on the VMD model.$|\alpha_{J/\psi p}|=3.83\pm 0.98$ am was obtained using GlueX [14] and SLAC [15] data. In our previous studies [5, 6], the same method was used to calculate the average scattering lengths$ |\alpha_{J/\psi p}|=3.85\pm0.96 $ am,$ |\alpha_{\psi(2s) p}|=1.31\pm0.92 $ am, and$ |\alpha_{\rho p}|=0.29\pm0.07 $ fm at the near-threshold. We found that the mass of the vector meson was inversely proportional to the scattering length of the V-p interaction,$ |\alpha_{\omega p}|>|\alpha_{\phi p}|>|\alpha_{J/\psi p}|>|\alpha_{\psi(2S) p}|>|\alpha_{\Upsilon p}| $ [5]. In this case, ρ was temporarily excluded owing to the particular situation.For the scattering length of the ϕ-p interaction, many research groups have also performed calculations and measurements. The scattering length
$ |\alpha_{\phi p} |\simeq2.37 $ was obtained by analyzing the QCD van der Waals potential [13], and in 2021, the real part of the scattering length of ϕ-p was found to be$ 0.85\pm0.34 $ fm via a$ pp $ collision by the ALICE Collaboration [16]. Note that these results go beyond the scattering length of the ϕ-p extracted from vector meson photoproduction data. Moreover, the scattering length of ϕ-p obtained by the VMD model was extracted from single data of vector meson photoproduction [1, 3, 4, 13]. Considering that the extraction of the ϕ-p scattering length from a single experimental data point may have an uncertainty, it is necessary to provide the distribution of the ϕ-p scattering length with energy at the threshold. Therefore, in this study, the two gluon exchange model [12] and pomeron model [17, 18] are established to predict the cross section of ϕ photoproduction. With the VMD model, the scattering length$ |\alpha_{\phi p}| $ is related to the photoproduction cross section and expressed as a function of R. Combined with the$ |\alpha_{\phi p}| $ extracted directly from the experimental data [2, 19, 20], the value of$ |\alpha_{\phi p}| $ at the near threshold R can be obtained. Here, R is the ratio of the final momentum$ |{\bf p}_3| $ to the initial momentum$ |{\bf p}_1| $ , which is directly proportional to the center of mass energy W.At present, research on the scattering length of vector mesons interacting with deuteron or helium nuclei composed of multiple nucleons is still limited. Considering the validity of the VMD model in describing the photoproduction process of vector meson and nucleus coherence [21–25], this study analyzes and calculates the scattering length of ϕ-deuteron (d). Fortunately, in 2007, the SLEP Collaboration [3] newly measured coherent ϕ photoproduction from deuterons at E=
$ 1.5 $ –$ 2.4 $ GeV with a forward angle and linearly polarized beam, which provided important experimental data for our study on the scattering length of ϕ-d. The findings of this paper not only contribute to our in-depth understanding of the ϕ-N interaction, but also provide a theoretical basis for future experimental measurements at JLab or EIC facilities [26, 27].This paper is organized as follows: Expressions for scattering length correlation, two gluon exchange, and pomeron models are described in Sec. II. The results of the scattering length of ϕ-N coherence are presented in Sec. III. Finally, a brief summary is provided in Sec. IV.
-
The total cross section of ϕ photoproduction at the near-threshold is related to the scattering length of the ϕ-N interaction (
$ |\alpha_{\phi N}| $ ) using the VMD model [9],$ \begin{aligned}[b] \left.\sigma ^{\gamma N \rightarrow \phi N}\right|_{{\rm t h r}}(R) &=\left.\frac{\left|\mathbf{\bf p}_3\right|}{\left|\mathbf{\bf p}_1\right|} \cdot \frac{4 \alpha_{\rm em} \pi^{2}}{g_{\phi}^{2}} \cdot \frac{{\rm d} \sigma^{\phi N \rightarrow \phi N}}{{\rm d} \Omega}\right|_{\rm {thr}} \\ &=R \cdot \frac{4 \alpha_{\rm em} \pi^{2}}{g_{\phi}^{2}} \cdot\left|\alpha_{\phi N}\right|^{2}, \end{aligned} $

(1) with the VMD coupling constant
$ g_{\phi} $ ,$ \begin{equation} g_{\phi}=\sqrt{\frac{\pi \alpha^{2}_{\rm em}m_{\phi}}{3\Gamma_{\phi \rightarrow e^+e^-}}}, \end{equation} $

(2) where N represent the nucleus,
$\alpha_{\rm em}$ is the fine coupling constant, R is the ratio of the final momentum$ |{\bf p}_3| $ to the initial momentum$ |{\bf p}_1| $ , and$ \Gamma_{e^{+}e^{-}}=1.27 $ keV is the lepton decay width taken from Ref. [2]. Using Eqs. (1) and (2), the scattering length$ |\alpha_{\phi N}| $ is$ \begin{equation} |\alpha_{\phi N}|=\frac{g_{\phi}}{2 \pi}\sqrt{\frac{\sigma^{\gamma N\rightarrow \phi N}}{\alpha_{\rm em} R}}. \end{equation} $

(3) In the center of mass frame, the initial and final momenta are
$ \begin{equation} \left|\mathbf{\bf p}_1\right|=\frac{1}{2 W} \sqrt{W^{4}-2\left(m_{1}^{2}+m_{2}^{2}\right) W^{2}+\left(m_{1}^{2}-m_{2}^{2}\right)^{2}}, \end{equation} $

(4) $ \begin{equation} \left|\mathbf{\bf p}_3\right|=\frac{1}{2 W} \sqrt{W^{4}-2\left(m_{3}^{2}+m_{4}^{2}\right) W^{2}+\left(m_{3}^{2}-m_{4}^{2}\right)^{2}}, \end{equation} $

(5) where W is the center of mass energy for the
$ \gamma p $ collision.The total cross section can be obtained by differential cross section integration from the four momentum
$t_{\rm min}(W)$ to$t_{\rm max}(W)$ , which can be given as$ \begin{equation} \sigma^{\gamma N \rightarrow \phi N}=\int_{t_{\rm min}(W)}^{t_{\rm max}(W)}\frac{{\rm d} \sigma^{\gamma N \rightarrow \phi N}}{{\rm d} t} {\rm d} t, \end{equation} $

(6) with
$ \begin{equation} t_{\max }\left(t_{\min }\right)=m_{1}^{2}+m_{3}^{2}-2 E_{1} E_{3} \pm 2\left|\mathbf{p}_{1}\right|\left|\mathbf{p}_{3}\right|, \end{equation} $

(7) where
$ E_{i}=\sqrt{|{\bf p}_i|^{2}+m_{i}^{2}} $ (i=1, 3). As the center of mass energy W approaches the threshold,$t_{\rm min}$ approaches$t_{\rm max}$ . Therefore, Eq. (6) is rewritten as$ \begin{equation} \left.\sigma\right|_{\rm t h r}=\left.4\left|\mathbf{p}_{1}\right| \cdot\left|\mathbf{p}_{3}\right| \frac{{\rm d} \sigma}{{\rm d} t}\right|_{\rm t h r} , \end{equation} $

(8) where
$|t_{\rm max} - t_{\rm min}|= \Delta t=4 |{\bf p}_3||{\bf p}_1|$ [9]. According to Eq. (1), the relation between the scattering length$ |\alpha_{\phi N}| $ and the differential cross section of ϕ photoproduction at the near-threshold can be expressed as$ \begin{equation} |\alpha_{\phi N}|=\frac{|{\bf p}_1|g_{\phi}}{\pi}\sqrt{\frac{1}{\alpha_{\rm em}}\frac{{\rm d} \sigma^{\gamma N \rightarrow \phi N}}{{\rm d} t}}, \end{equation} $

(9) In keeping with Eq. (3), the above formula is expressed as a function of R,
$ \begin{equation} |\alpha_{\phi N}|=\frac{|{\bf p}_3|g_{\phi}}{R \pi}\sqrt{\frac{1}{\alpha_{\rm em}}\frac{{\rm d} \sigma^{\gamma N \rightarrow \phi N}}{{\rm d} t}}. \end{equation} $

(10) -
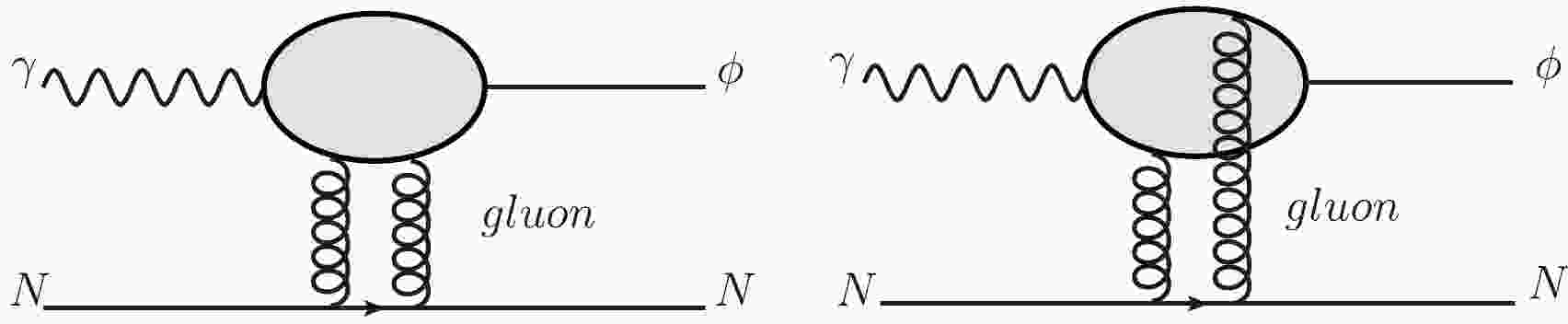
Photons split into a pair of dipoles, which exchange two gluons to scatter protons and finally form the meson ϕ in the two gluon exchange model, as shown in Fig. 1. In lowest order perturbative QCD, the differential cross section obtained from the ϕ photoproduction amplitude is [17]
$ \begin{equation} \frac{{\rm d} \sigma}{{\rm d} t}=\frac{\pi^{3} \Gamma_{e^+ e^-} \alpha_{s}}{6 \alpha m_{s}^{5}}\left[x g\left(x, m_{\phi}^{2}\right)\right]^{2} \exp \left(b_{0} t\right), \end{equation} $

(11) where the QCD coupling constant
$ \alpha_{s}=0.701 $ is from Ref. [28],$ m_{s} $ is the mass of the strange quark,$ m_{\phi}=1.019 $ GeV is the mass of the meson ϕ, and$ b_{0} $ is the slope.$ xg(x,m_{\phi}^{2})=A_{0}x^{A_{1}}(1-x)^{A_{2}} $ is the parameterized gluon distribution function, and$ A_{0} $ ,$ A_{1} $ , and$ A_{2} $ are free parameters. The total cross section of ϕ photoproduction can be obtained by integrating Eq. (11) from$t_{\rm min}(W)\rightarrow t_{\rm max}(W)$ $ \begin{equation} \sigma^{\gamma p \rightarrow \phi p}=\int_{t_{\rm min}(W)}^{t_{\rm max}(W)}\frac{{\rm d} \sigma^{\gamma p \rightarrow \phi p}}{{\rm d} t}{\rm d} t. \end{equation} $

(12) -
Figure 2 represents the
$ \gamma p $ $ \rightarrow $ $ \phi p $ reaction process of the pomeron model [17, 18], where the differential cross section of ϕ photoproduction is written as$ \begin{equation} \frac{\mathrm{d} \sigma}{\mathrm{d} t}=\frac{81 m_{\phi}^{3} \beta^{4} \mu_{0}^{4} \Gamma_{\mathrm{e}^+ \mathrm{e}^-}}{\pi \alpha_{\rm em} }\left(\frac{s}{s_{0}}\right)^{2\alpha(t)-2}F_{1}(t), \end{equation} $

(13) with
$ \begin{equation} F_{1}(t)= \left(\frac{F(t)}{\left(Q^{2}+m_{\phi}^{2}-t\right)\left(Q^{2}+2 \mu_{0}^{2}+m_{\phi}^{2}-t\right)}\right)^{2}, \end{equation} $

(14) where
$ Q^{2} $ is the square of the virtual photon,$ s_0=4 $ GeV$ ^2 $ ,$\alpha_{\rm em}$ is the fine coupling constant, and$ \mu^{2}=1.1 $ GeV$ ^{2} $ .$ F(t) $ is the form factor and expressed as$ \begin{equation} F(t)=\frac{4 m_{\mathrm{N}}^{2}-2.8 t}{\left(4 m_{\mathrm{N}}^{2}-t\right)(1-t / 0.7)^{2}}, \end{equation} $

(15) where
$ m_{N} $ is the mass of a proton or deuteron. The Regge trajectory$ \alpha(t)=1.08+0.25t $ can be obtained from Ref. [29].In our previous study [12],
$ \beta^{2}=4 $ GeV$ ^{-2} $ was corrected by the nucleon and nucleon scattering amplitude from Ref. [29]. In this study, β is a free parameter and obtained by fitting the experimental data of ϕ photoproduction. -
In our previous study [12], the two gluon exchange model was established to effectively extract the mass radius of the proton, which is extremely proximate to that extracted directly from the CLAS [19] and LEPS [20] data. The free parameters,
$ A_0 $ ,$ A_1 $ ,$ A_2 $ , and$ b_0 $ , contained in this model were obtained via global fitting of the total [2, 30–34] and differential [19, 20] cross sections of ϕ photoproduction data. In addition, the pomeron model was introduced as an auxiliary model in contrast to the two gluon exchange model. In this study, the two gluon exchange model is still used to calculate the scattering length of the ϕ-p interaction. In addition, β in the pomeron model is considered a free parameter obtained by fitting the total [2, 30–34] and differential [19, 20] experimental cross section data. The parameters present in the two gluon exchange and pomeron models are shown in Table 1. Figures 3 and 4 show the total and differential cross sections of ϕ photoproduction predicted by the two gluon exchange and pomeron models at the near-threshold, which are in good agreement with experimental data on ϕ. Based on the two models, we assume that the cross section of ϕ photoproduction can be reliably predicted.$ A_{0} $ 

$ A_{1} $ 

$ A_{2} $ 

$ b_{0} $ /GeV

$ ^{-2} $ 

$ \chi^{2}/ $ d.o.f

$ 0.36 \pm 0.04 $ 

$ -0.055 \pm 0.003 $ 

$ 0.12 \pm 0.03 $ 

$ 3.60\pm0.04 $ 

$ 2.87 $ 

β /GeV $ ^{-1} $ 

− − − $ \chi^{2}/ $ d.o.f

$ 1.919\pm0.011 $ 

− − − $ 9.88 $ 

Table 1. Relevant parameters for the two gluon exchange model are in the first row, and the second row is for the pomeron model.
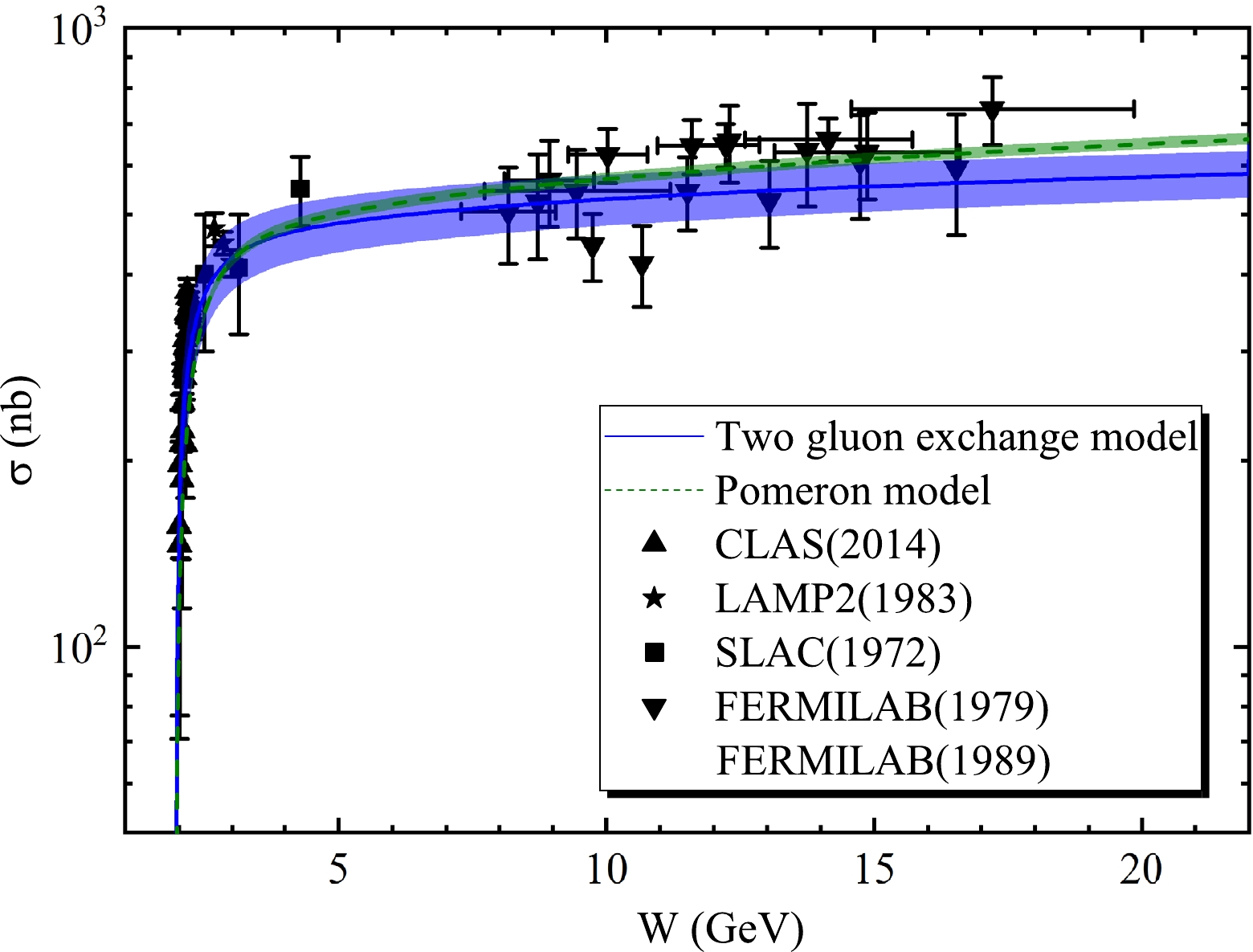
Figure 3. (color online) Total cross section of ϕ photoproduction as a function of the center of mass energy W. The solid-line (blue) and dashed line (olive-green) represent the two gluon exchange and pomeron models, respectively.
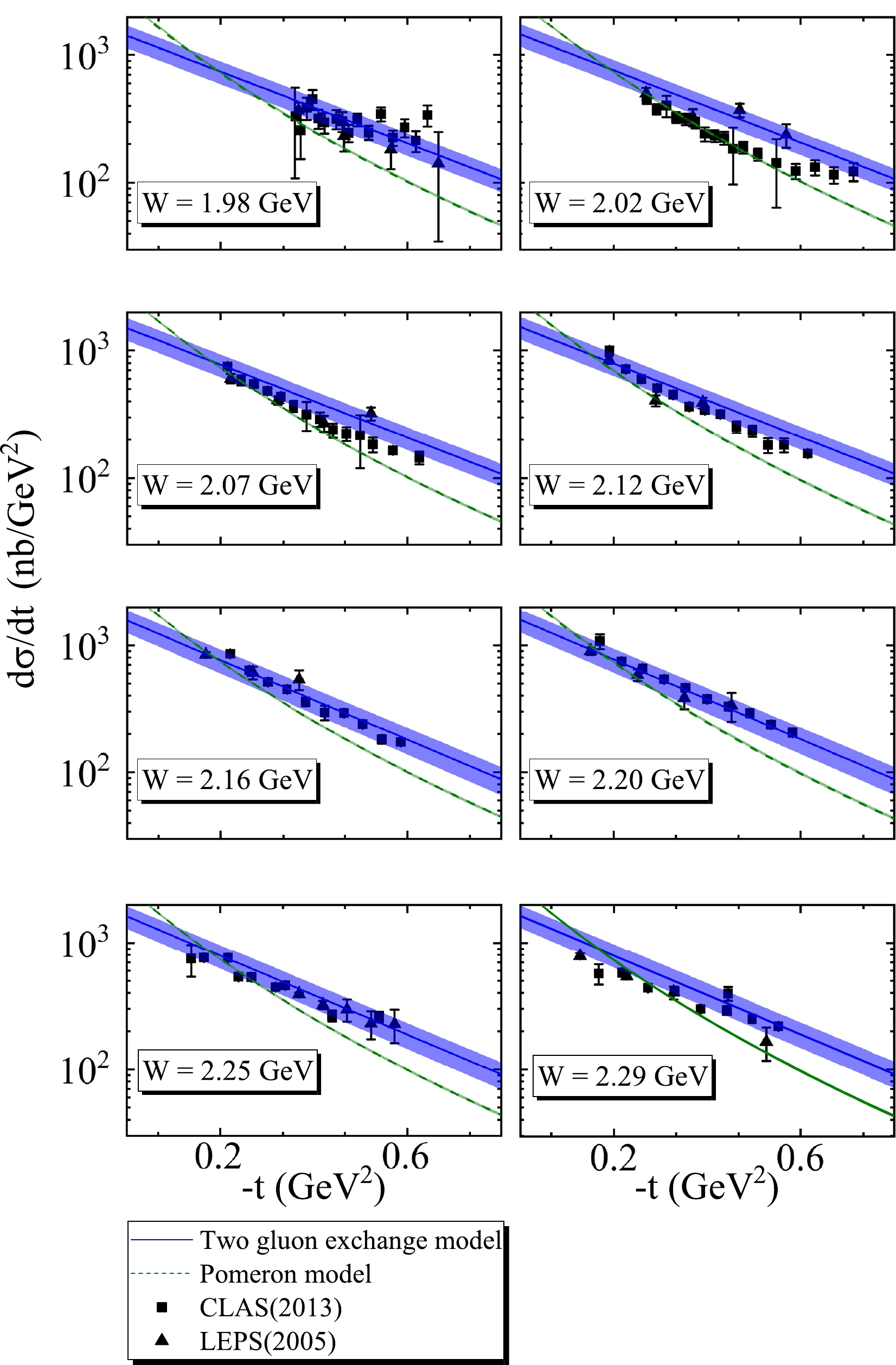
Figure 4. (color online) Differential cross sections of the channel
$ \gamma p \rightarrow \phi p $ as a function of$ -t $ at different W values. Here, the notations are the same as in Fig. 3.The scattering length
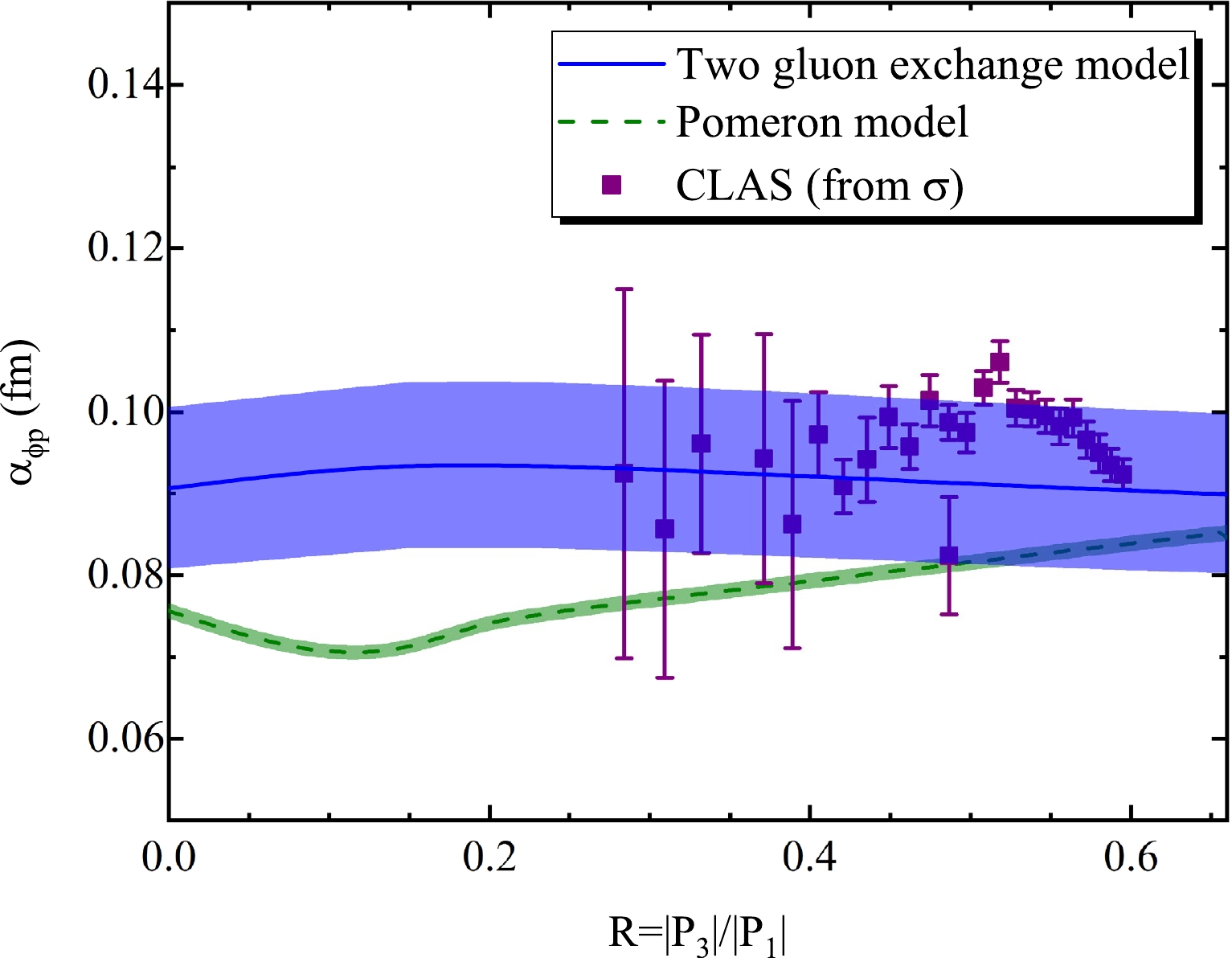
$ |\alpha_{\phi p}| $ obtained from the differential cross section of ϕ photoproduction has a slow upward trend with R, which can be observed in Fig. 5. Here, the R interval is selected as$ [0,0.66] $ . The blue line is$ |\alpha_{\phi p}| $ based on the two gluon exchange model, with an average scattering length of$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}=0.102\pm0.011 $ fm. The olive-green dashed line is$ |\alpha_{\phi p}| $ obtained from the pomeron model with$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}=0.087\pm0.001 $ fm, which is smaller than the result from the two gluon exchange model. The magenta circle represents$ |\alpha_{\phi p}| $ extracted directly from the CLAS [19] and LEPS [20] data. The$ |\alpha_{\phi p}| $ corresponding to each center of mass energy W is listed in Table 2, and$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}=0.106\pm0.005 $ fm. Overall,$ |\alpha_{\phi p}| $ obtained from the pomeron model is not in good agreement with that extracted directly from the experiment. In contrast,$ |\alpha_{\phi p}| $ based on the two gluon exchange model agrees well. This indicates that the scattering length derived from the differential cross section predicted by the two gluon exchange model is reliable.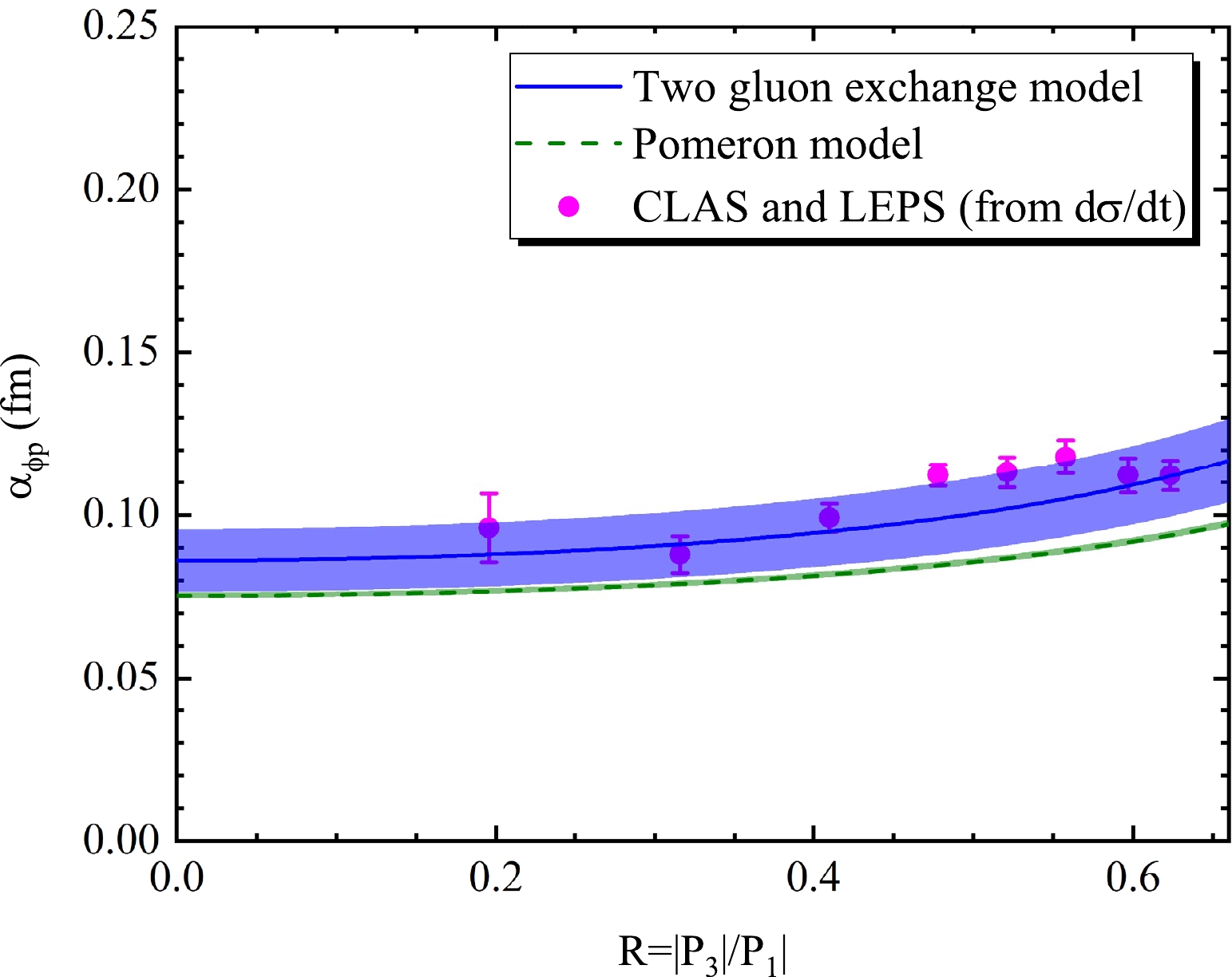
Figure 5. (color online) Function of
$ |\alpha_{\phi p}| $ with R from the differential experimental cross section. The blue-line is the result derived from the two gluon exchange model, and the olive green dashed-line shows the result based on the pomeron model. The magenta circle is extracted directly from CLAS [19] and LEPS [20] data.W /GeV $ 1.98 $ 

$ 2.02 $ 

$ 2.07 $ 

$ |\alpha_{\phi p}| $ /fm

$ 0.096 \pm 0.011 $ 

$ 0.088 \pm 0.006 $ 

$ 0.099 \pm 0.004 $ 

W /GeV $ 2.12 $ 

$ 2.16 $ 

$ 2.20 $ 

$ |\alpha_{\phi p}| $ /fm

$ 0.109 \pm 0.003 $ 

$ 0.113 \pm 0.005 $ 

$ 0.118 \pm 0.005 $ 

W /GeV $ 2.25 $ 

$ 2.29 $ 

− $ |\alpha_{\phi p}| $ /fm

$ 0.112\pm0.005 $ 

$ 0.108\pm0.005 $ 

− As a comparison,
$ |\alpha_{\phi p}| $ can also be calculated from the total cross section of ϕ photoproduction. The$ |\alpha_{\phi p}| $ as a function of$ R\in[0,0.66] $ directly calculated from CLAS data [2] and based on the total cross sections predicted by the two models is shown in Fig. 6.$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}= 0.091\pm 0.010 $ fm based on the two gluon exchange model, and$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}=0.081\pm0.001 $ fm for the pomeron model.$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle}=0.096\pm0.010 $ fm is obtained directly from the total experimental cross section of CLAS data [2]. Here, the same problem arises.$ |\alpha_{\phi p}| $ based on the pomeron model is obviously small and in poor agreement with that obtained directly from CLAS data [2]. This indicates that the pomeron model's overall prediction is insufficient. Therefore,$ |\alpha_{\phi p}| $ obtained by the pomeron model is ignored in the discussion below.The above discussion shows differences in the scattering length obtained from the total and differential cross sections of ϕ photoproduction at
$ R\in[0,0.66] $ , which can be seen in Table 3.$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle} $ obtained directly from experimental data [2, 19, 20] is slightly larger than that based on the two gluon exchange model but within the error range.$ \sqrt{\langle |\alpha^{2}_{\phi p}|\rangle} $ based on the differential cross section is barely larger than that obtained from the total cross section. This is because of the lack of experimental data. In particular, in the total cross section, the behaviour closest to the threshold scattering length cannot be observed. However, when the error bars are considered, the difference is completely eliminated, and the average scattering lengths based on the differential and total cross sections are almost identical. Therefore, we calculate the root-mean-square of the scattering length obtained from the total and differential cross sections. The final scattering length of the ϕ-p interaction is$ 0.10\pm0.01 $ fm.Model Scattering length $/\mathrm{fm}$ 

${\rm d} \sigma / {\rm d} t$ 

σ Two gluon exchange model $ 0.102 \pm 0.011 $ 

$ 0.091 \pm 0.010 $ 

Extraction from experimental data $ 0.106 \pm 0.005 $ 

$ 0.096 \pm 0.010 $ 

A comparison of the scattering lengths of ϕ-p obtained in this study with those of other groups [2–4, 13, 16] is shown in Fig. 7. Our result is roughly in the middle, between that obtained by the LEPS laboratory [3], QCD sum rules [4], and Strakovsky et al. [2]. Particular attention should be paid to the result of QCD sum rules [4],
$ \alpha_{\phi p}=-0.15\pm0.02 $ fm, which was obtained by introducing the vector-current nucleon forward scattering amplitude relationship without any experimental data. Strakovsky et al. [2] also used the VMD model to relate σ to the scattering length and obtained$ |\alpha_{\phi p}|=0.063\pm0.012 $ fm by fitting an odd power. However, two relatively large results clearly go beyond our normal understanding of the scattering length of ϕ-p. A result from QCD van der Waals [13] was$ |\alpha_{\phi p} |\simeq2.37 $ fm, and a real part of the scattering length of the ϕ-p interaction calculated by the ALICE Collaboration [16] from the cross section of high-multiplicity$ pp $ collisions was$ 0.85\pm0.34 $ fm. We suppose that different reactions should exist; hence, these two results are ignored for the time being.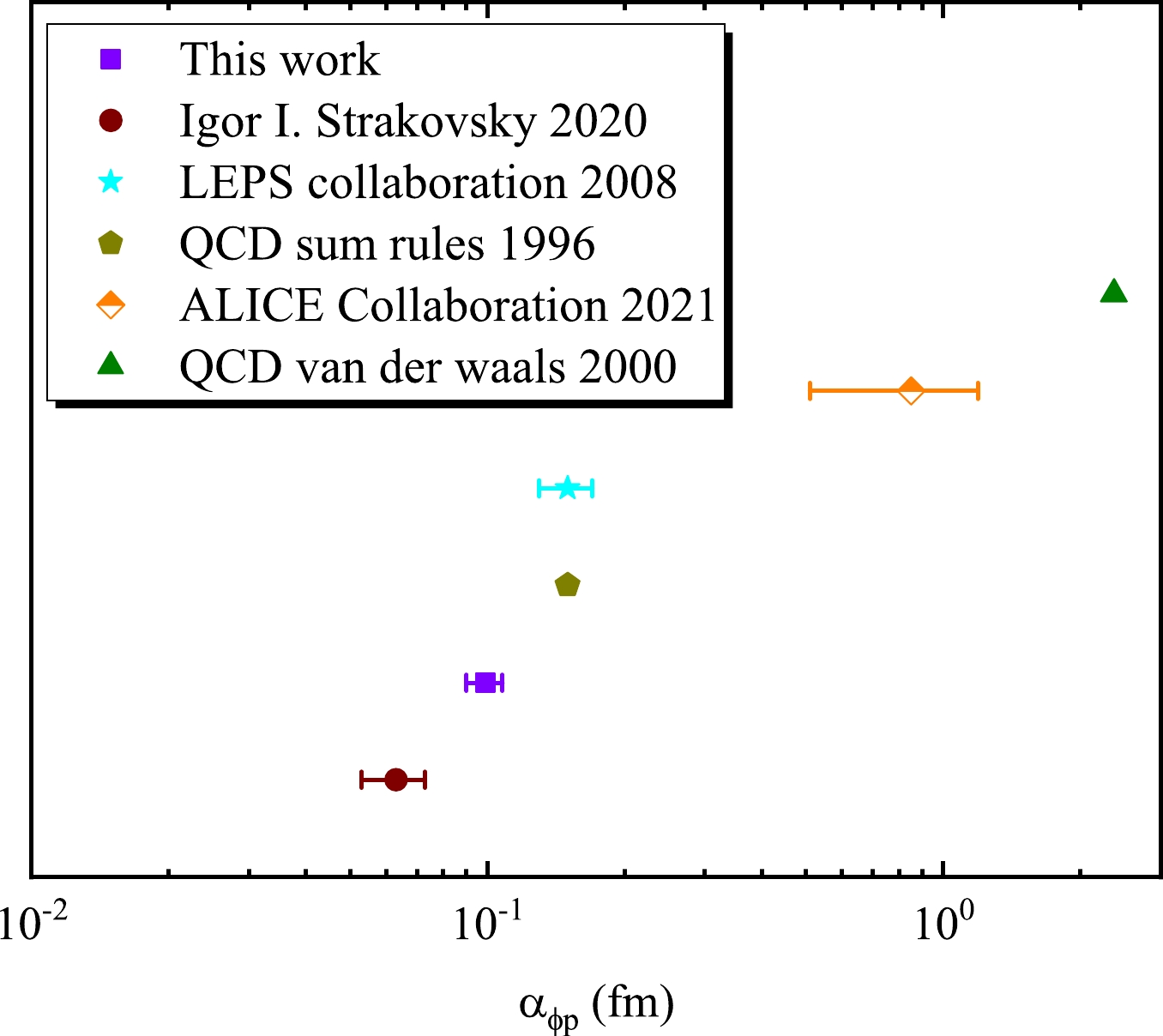
Figure 7. (color online) Scattering length obtained in this study is compared with the absolute value obtained by other groups [2–4, 13]. The purple square is
$ |\alpha_{\phi p}|=0.10\pm0.01 $ fm. The burgundy circle is$ |\alpha_{\phi p}|=0.063\pm0.01 $ fm, which was obtained by CLAS data analysis with the VMD model [2]. The LEPS laboratory [3] obtained$ |\alpha_{\phi p}|=0.15 $ fm, which is represented by a cyan pentagram. The dark yellow pentagon represents$ |-0.15| \pm 0.02 $ fm, obtained with QCD sum rules [4]. The olive-green triangle represents$ |\alpha_{\phi p} |\simeq2.37 $ fm, obtained by QCD van der Waals [13]. The orange diamond is the result of the ALICE Collaboration [16].In our previous studies [5, 6], the scattering lengths of
$ J/\psi $ -p,$ \psi(2S) $ -p, and ρ-p were systematically studied. In addition, relative vector meson scattering lengths have been calculated by other research groups [2–4, 7, 8]. The scattering lengths calculated by different groups for vector mesons with the proton interaction are shown in Fig. 8. The red line represents the proportional relationship between the scattering length$ |\alpha_{Vp}| $ and$ \exp{(1/m_{V})} $ .$|\alpha_{\phi p}|= 0.10\pm0.01$ fm from this study intersects this line, demonstrating that our analysis is reliable.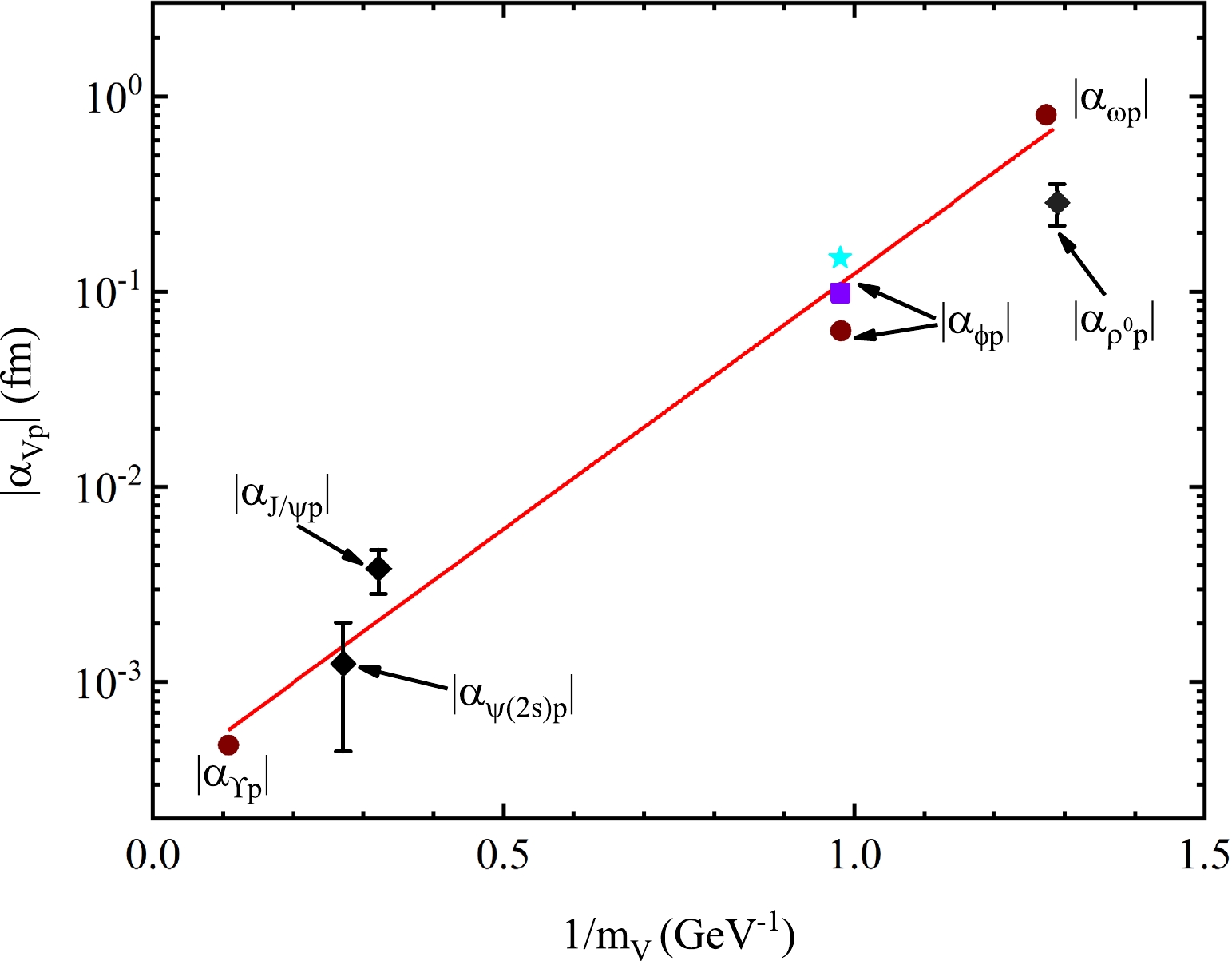
Figure 8. (color online) Scattering length of
$ |\alpha_{V p}| $ , where V is a vector meson. The purple square represents$ |\alpha_{\phi p}|=0.10\pm0.01 $ fm. The result indicated by the black diamonds originate from our previous studies [5, 6]. The burgundy circles are the results of Refs. [2, 7, 8]. The cyan pentagram represents the result from the LEPS laboratory [3]. -
From the analysis, we find that the slope of the cross section distribution of
$ \gamma d\rightarrow \phi d $ is larger than that of$ \gamma p \rightarrow \phi p $ ; hence, it is inappropriate to describe ϕ-d based on the two gluon exchange model with$ b_{0} $ =$ 3.6 $ GeV$ ^{2} $ . The gluon distribution function$ xg(x,m_{\phi}^{2}) $ obtained from ϕ-p is preserved. That is,$ A_{0} $ ,$ A_{1} $ , and$ A_{2} $ are retained, while$ b_{0} $ is set as a free parameter and re-fitted by LEPS [3] data. The relevant fitting results are shown in Figs. 9 and 10, which are in good agreement with the LEPS data, and the parameters are shown in Table 4. The differential cross sections of ϕ photoproduction from deuterons from the LEPS data are distributed at$ W\in[3.10,3.50] $ GeV, corresponding to$ R\in[0.54,0.76] $ . Based on Eq. (10), the scattering length$ |\alpha_{\phi d}| $ as a function of R is shown in Fig. 11.$ |\alpha_{\phi d}| $ obtained directly from the LEPS data is shown in Table 5, and the average scattering length$\sqrt{\langle |\alpha^{2}_{\phi d}|\rangle}= 0.015\pm 0.002$ fm. At$ R\in[0.54,0.76] $ ,$\sqrt{\langle |\alpha^{2}_{\phi d}|\rangle}=0.016\pm 0.002$ fm from the two gluon exchange model. The two average scattering lengths are extremely adjacent, with a difference of only$ 0.001 $ fm, which indicates that$ |\alpha_{\phi d}| $ obtained based on the model is reliable. Based on this, the average scattering length at$ R\in[0,0.66] $ is calculated to be$ 0.014\pm0.002 $ using the two gluon exchange model. Here,$ R\in[0,0.66] $ is selected for ϕ-d for consistency with ϕ-p.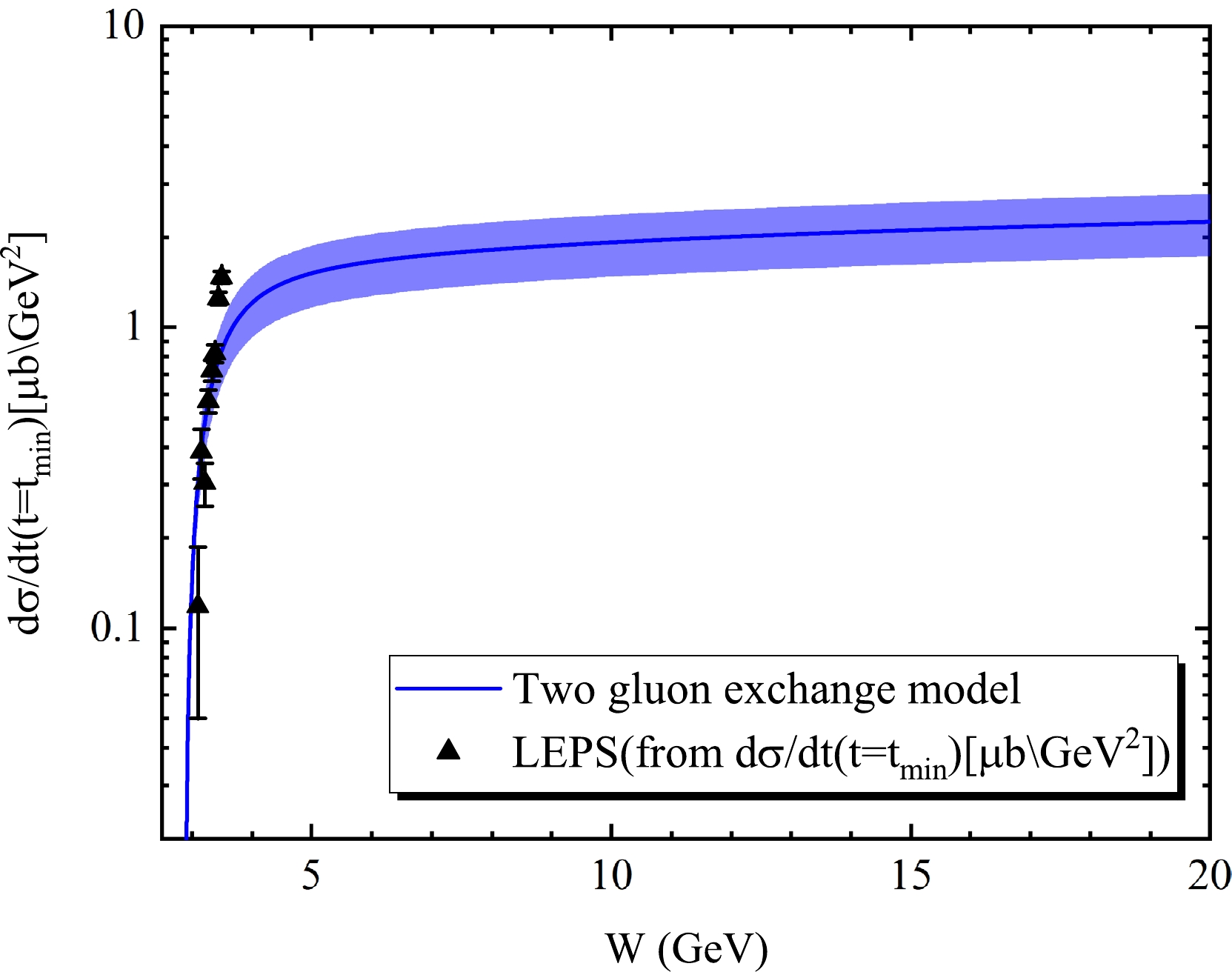
Figure 9. (color online)
${\rm d} \sigma/{\rm d}t(t=t_{\rm min})$ of ϕ photoproduction from deuterons as a function of the center of mass energy W. The solid-line (blue) is from the two gluon exchange model, and the black triangle is from the LEPS Collaboration [3].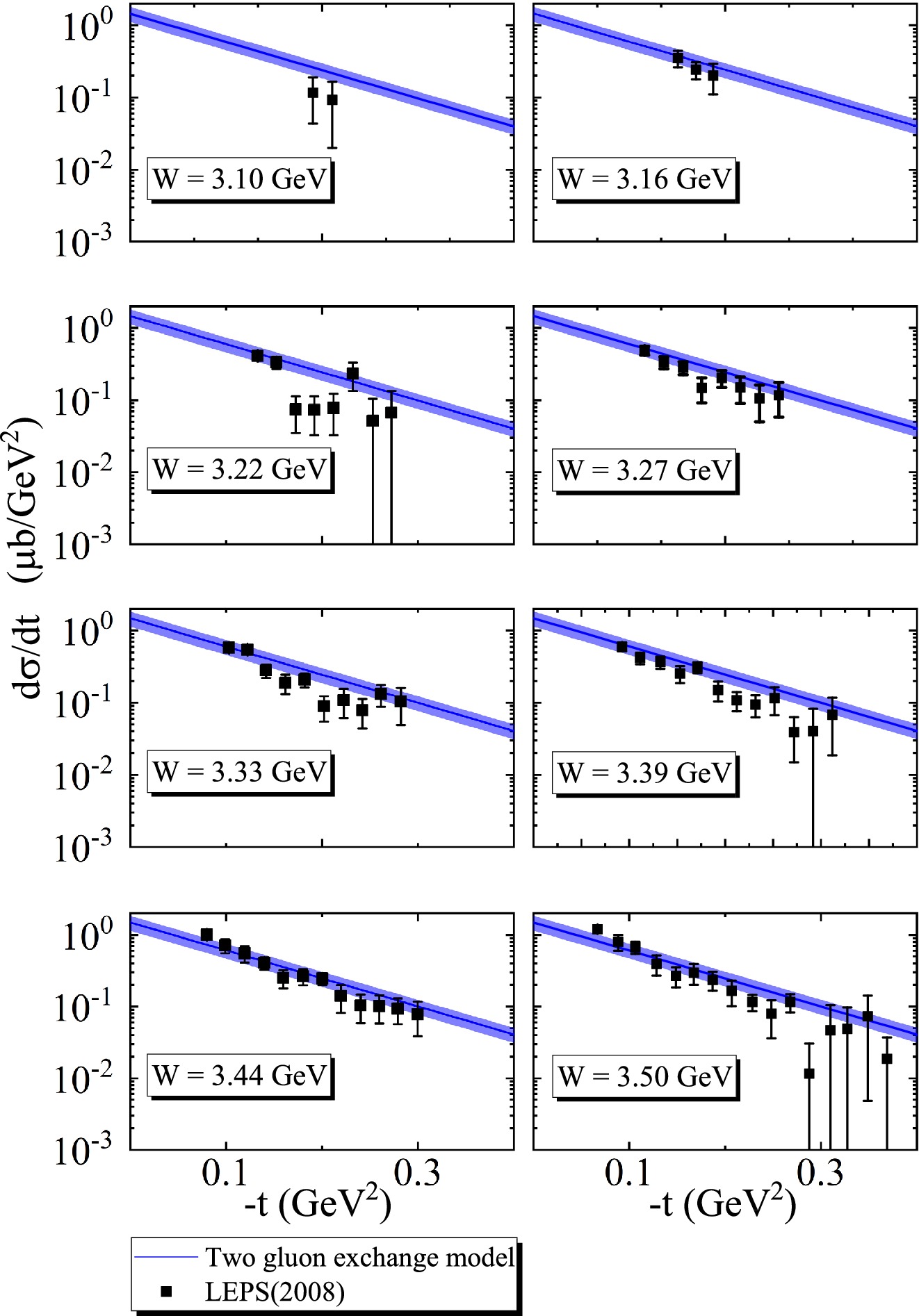
Figure 10. (color online) Differential cross sections of ϕ based on the two gluon exchange model (blue line) as a function of
$ -t $ at different W values. Here, the black square represents the experimental data of$ \gamma d \rightarrow \phi d $ from the LEPS Collaboration [3].$ A_{0} $ 

$ A_{1} $ 

$ A_{2} $ 

$ b_{0} $ /GeV

$ ^{-2} $ 

$ \chi^{2} / $ d.o.f

$ 0.36 \pm 0.04 $ 

$ -0.055 \pm 0.003 $ 

$ 0.12 \pm 0.03 $ 

$ 9\pm0.29 $ 

$ 0.17 $ 

Table 4. Parameters
$ A_{0} $ ,$ A_{1} $ ,$ A_{2} $ ,$ b_{0} $ , and$ \chi^{2} / $ d.o.f are for the process$ \gamma d \rightarrow \phi d $ .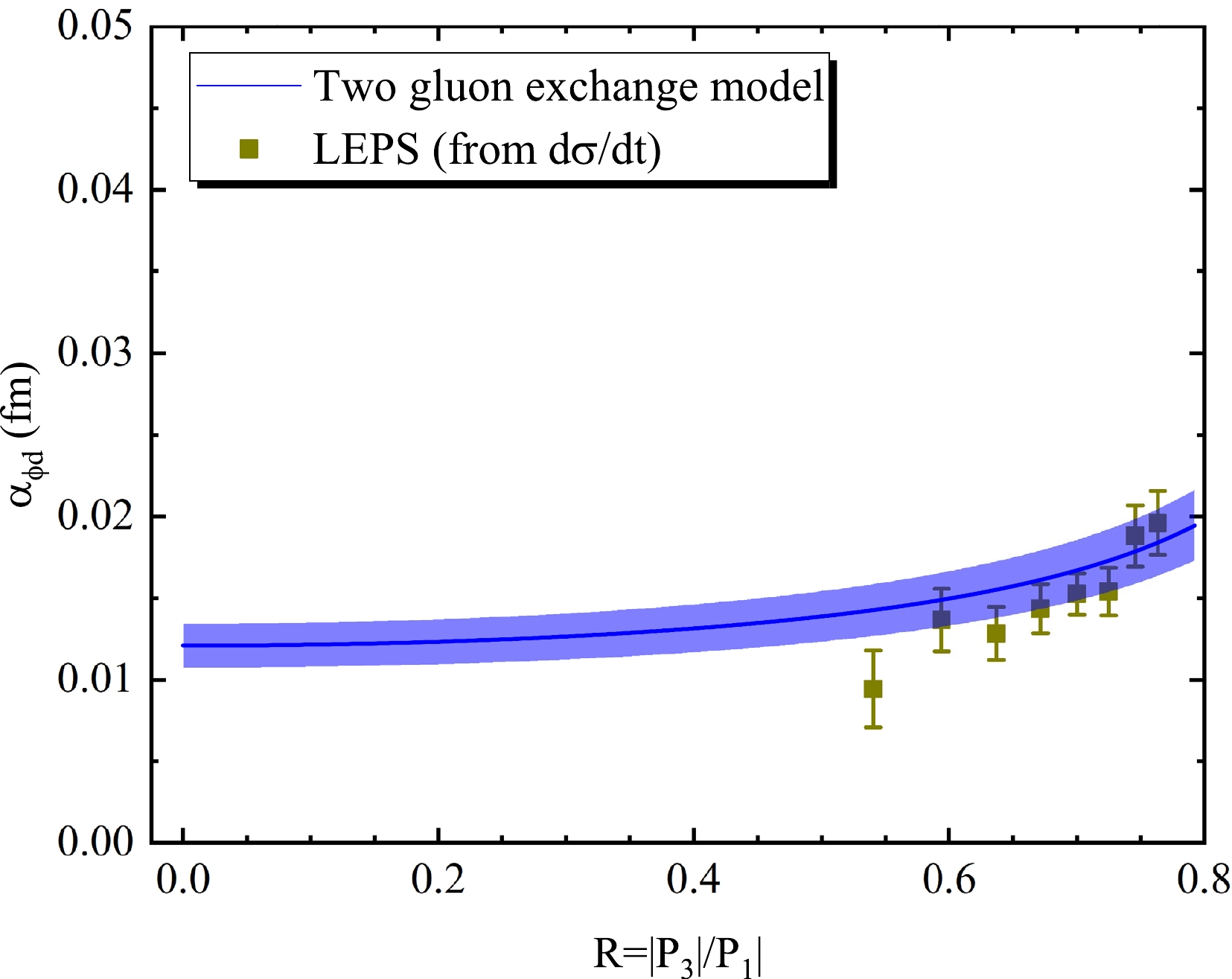
Figure 11. (color online) Function of
$ |\alpha_{\phi d}| $ with R based on the two gluon exchange model (blue line). The dark-yellow squares are the results from LEPS [3] data.W /GeV $ 3.10 $ 

$ 3.16 $ 

$ 3.22 $ 

$ |\alpha_{\phi d}|/{\rm{fm}} $ 

$ 0.009 \pm 0.002 $ 

$ 0.014 \pm 0.002 $ 

$ 0.013 \pm 0.002 $ 

W /GeV $ 3.28 $ 

$ 3.33 $ 

$ 3.39 $ 

$ |\alpha_{\phi d}|/{\rm{fm}} $ 

$ 0.014 \pm 0.001 $ 

$ 0.015 \pm 0.001 $ 

$ 0.015 \pm 0.001 $ 

W /GeV $ 3.44 $ 

$ 3.50 $ 

- $ |\alpha_{\phi d}| /{\rm{fm}} $ 

$ 0.019\pm0.002 $ 

$ 0.020\pm0.002 $ 

- Table 5. Scattering length of ϕ-d is derived from the differential experimental cross section from LEPS [3] data, where the average is
$ 0.015\pm0.002 $ fm.According to these results,
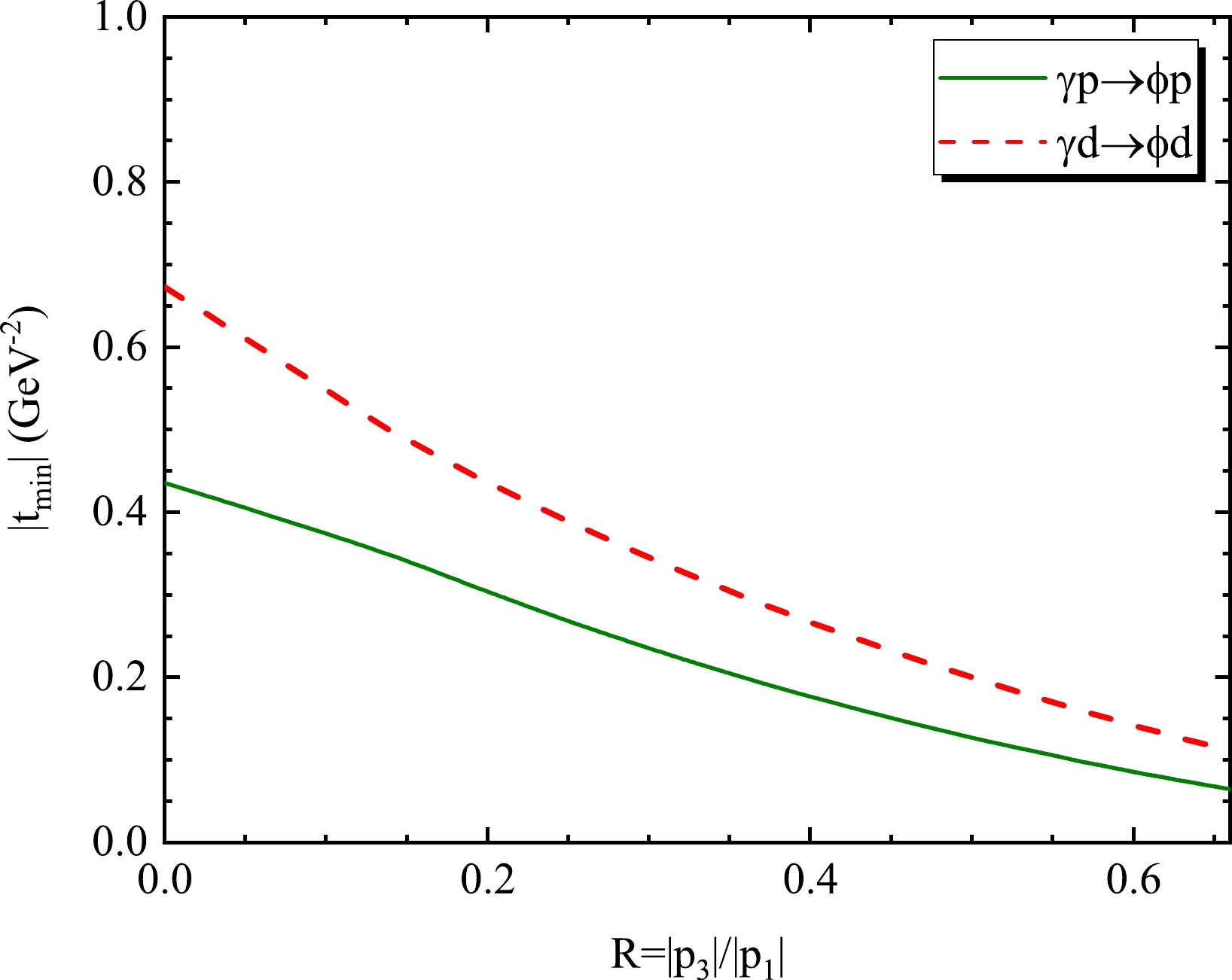
$ |\alpha_{\phi d}| $ is relatively smaller than$ |\alpha_{\phi p}| $ As shown in Figs. 4 and 10, the differential cross sections of ϕ-d and ϕ-p photoproduction belong to the same order of magnitude, and there is a slight distinction between them. However, the influence of$|t_{\rm min}|$ on the differential cross section is enormous owing to the diverse nucleons or nuclei interacting with ϕ. Figure 12 comprehensively demonstrates this difference.$|t_{\rm min}|$ of ϕ-d is larger than that of ϕ-p at$ R\in[0,0.66] $ . Furthermore, consider the slope of the differential cross section of ϕ-d to be steeper. Therefore,$ |\alpha_{\phi d}| $ $ < $ $ |\alpha_{\phi p}| $ is adequately explained. -
In this study, based on the experimental data of ϕ photoproduction at the near threshold [2, 19, 20], the interaction between the ϕ meson and nucleus is systematically investigated under the framework of the VMD model. Specifically, the average scattering length of the ϕ-p interaction is calculated to be
$ 0.10\pm0.01 $ fm, which satisfies$ |\alpha_{Vp}| $ proportional to$ \exp{(1/m_{V})} $ . Note that our conclusions are similar to the results given by the VMD model [2, 3] and QCD sum rules [4]; however, they are different from the results obtained by the ALICE Collaboration [16]. This may be due to different reaction processes; the ALICE Collaboration measured a complete two-body ϕ-N interaction, whereas the results obtained using the VMD model may refer to the properties of ϕ embedding into nucleons [16].Moreover, the scattering length of the ϕ and deuteron interaction is investigated for the first time, and the average scattering length
$ |\alpha_{\phi d}| $ is calculated to be$ 0.014\pm0.002 $ fm, which is nearly seven times smaller than$ |\alpha_{\phi p}| $ . This result indicates that the ϕ-d coupling is considerably weaker than that of ϕ-p. One possible explanation is that because the deuteron is composed of two nucleons, the ϕ meson is overall more fully embedded in the deuteron than in the nucleon [16], making the ϕ-d scattering length smaller. Of course, this is still an open question, and further explanations and discussions are required.It should be noted that although the pomeron model and parameterized two gluon exchange model can describe vector meson photoproduction data well, there are usually contributions from intermediate exchange mesons or nucleon resonances in the low energy region. For example, in Refs. [35, 36], the contribution of
$ \pi^{0} $ and η meson exchange to the cross section of vector meson photoproduction was discussed. In Refs. [37–40], the role of the intermediate nucleon resonances and direct ϕ meson radiation via proton exchanges was also studied. These results indicate that more research on the production mechanism of vector meson photoproduction at low energies is still needed, which will be helpful to more accurately explain the interaction between a vector meson and a nucleus.To study these issues more accurately, it is necessary to measure more accurate experimental data on vector meson photoproduction or electroproduction. At present, EIC facilities [26, 27] in China and the United States have listed nuclear structure and properties as important scientific objectives, and the ϕ-N interaction is an essential direction of study. Our results can provide a crucial reference and basis for detecting the scattering length of the ϕ-N interaction more accurately in the future.
Analysis of the interaction between the ϕ meson and nucleus
- Received Date: 2022-08-25
- Available Online: 2023-01-15
Abstract: In this study, we systematically investigate the ϕ meson and nucleus interaction by analyzing and fitting the cross sections of


 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: