-
Quarks are generally believed to appear within hadronic matter, due to the feature of color confinement. However, it is expected, with increasing density, that the basic constituent of hadronic matter, i.e. hadrons, might squeeze out to form deconfined quark matter at low temperatures. About forty years ago, Witten first conjectured that strange quark matter (SQM) [1], consisting of roughly equal number of up, down, and strange quarks, could be the true ground state of strong interaction [2].
Since SQM could be absolutely stable, there might be compact objects with a quark core or even completely made of quarks and leptons, i.e., the so-called strange stars [3–7]. Recently, comparison of the theoretical calculations in a model-independent way with astrophysical observations suggests that there might be a quark matter core in the maximally massive neutron stars [8]. Several studies also imply that strange stars can coexist with neutron stars [9–16]. One important feature of such stars is the associated strong magnetic field, with strength of the order
$ 10^{11}\sim10^{13} $ G on the surface of pulsars [17], or even reaching$ 10^{14}\sim 10^{15} $ G in some magnetars [18]. In the core of compact stars, the magnetic field strength is estimated to be as high as$ 10^{18}\sim 10^{20} $ G [19–23]. Except for stellar objects, the magnetic field strength produced in heavy ion collisions can be as strong as$ 10^{18}\sim 10^{19} $ G [24–28]. However, let us emphasize that estimates of the largest value of magnetic field$ B_m $ inside the compact stars exist, see for example Ref. [29] and references therein; however, these estimates have some dependence on the model used for the equation of state of bulk matter. In this study we take the$ B_m=O(10^{18}\; \text{G}) $ as a conservative estimate of the maximum value of$ B_m $ , and use larger values of$ B_m $ only for illustrative purposes; see Fig. 5.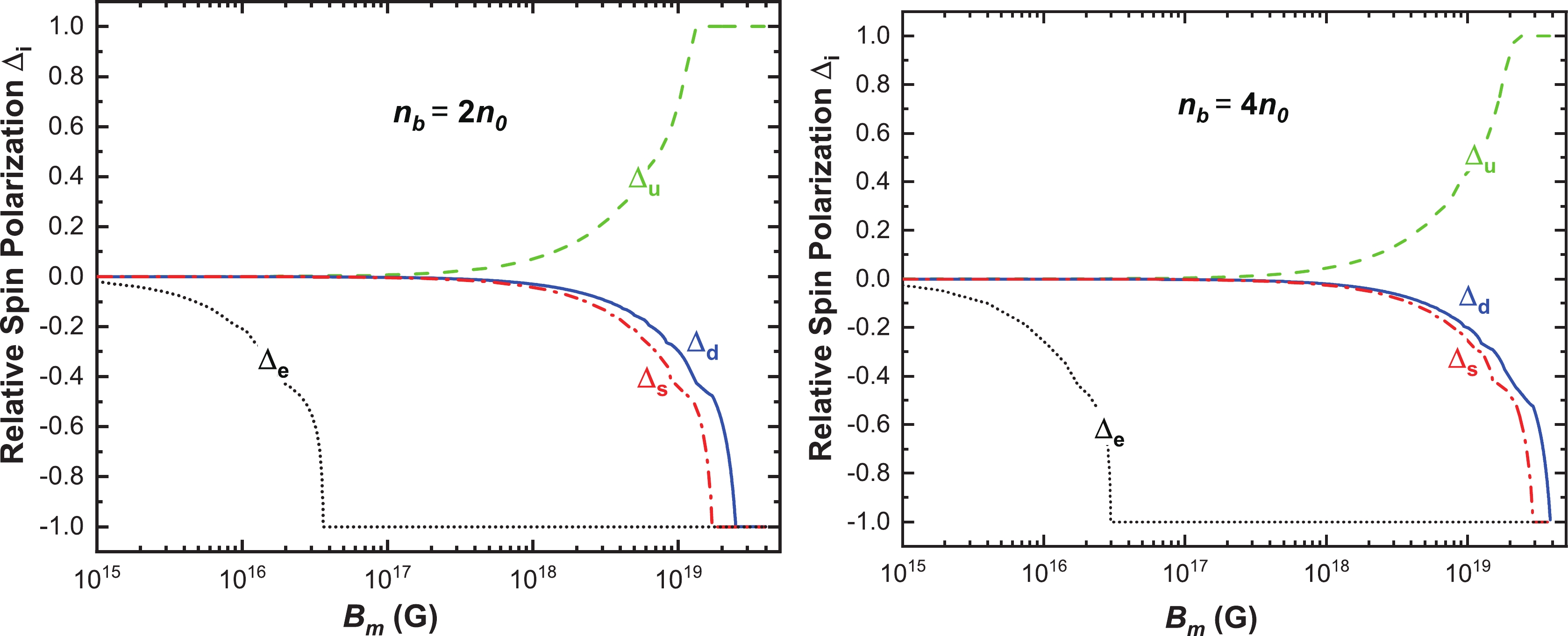
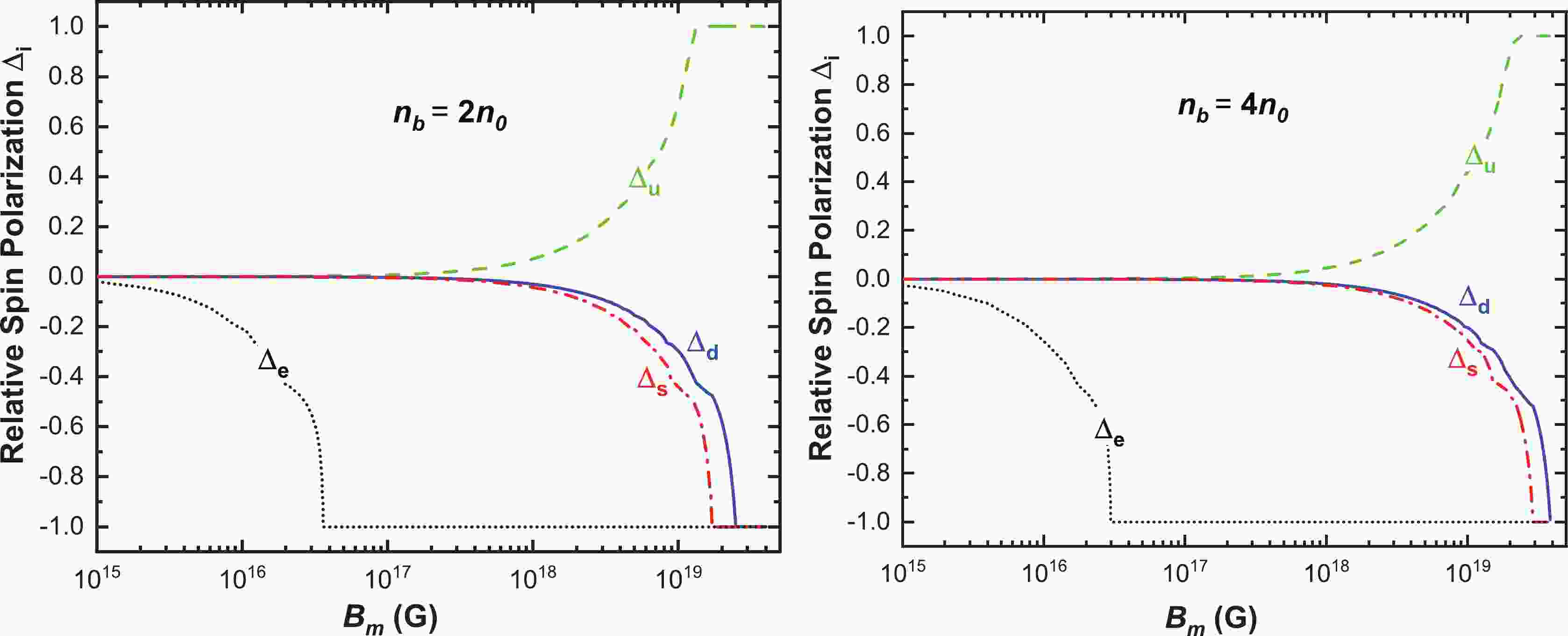
Figure 5. (color online) Variation of the relative spin polarization for up, down, and strange quarks, and electrons, with respect to the magnetic field strength at
$ n_b=2n_0 $ (left panel) and$ n_b=4n_0 $ (right panel).The presence of a strong magnetic field introduces Landau levels for the charged particles and hence has significant effects on the stability of SQM [30–32]. The properties of SQM in a strong magnetic field have attracted increasing interest over the past few decades; for example, the effects of an external magnetic field on the symmetry energy [33, 34], equation of state [35] and surface tension of quark matter [36], and r-mode instability [37, 38] as well as structure properties of strange stars [39–43], etc. In addition, the presence of a magnetic field can also affect the in-medium chiral condensates [44], and hence the critical temperature of the chiral phase transition [45–52], as well as the deconfinement transition [53–57]. Due to the intractable nature of quantum chromodynamics (QCD) in the nonperturbative regime, we need to find a proper way to mimic the strong interactions between quarks. The medium-dependence of quarks can be taken into account by considering a quark mass dependent on chemical potential and/or temperature in the quasiparticle model [58]. In this case, however, special attention should be paid to the thermodynamic consistency of the phenomenological models [59–64]. To confine quarks, an effective bag constant is required in the nonperturbative regime [65]①. Since the quark masses are dependent on chemical potential and/or temperature, the additional effective bag constant should also be simultaneously dependent on chemical potential and/or temperature in order to satisfy the fundamental relations of thermodynamics [66, 67]. Following the original idea in Refs. [68, 69], the quasiparticle model with a fixed strong coupling has been used to study the finite-size strangelets [70] and the medium effects on the surface tension of strangelets [71, 72]. Later, this model is extended to include the running strong coupling with a chemical-potential-dependent renormalization subtraction point, which is constrained by the Cauchy condition in the chemical potential space [73].
In this work, we restrict ourselves to the deconfined SQM and study the effect of a magnetic field on the properties of SQM, especially on the behavior of maximum Landau levels, particle fractions, relative spin polarization, and sound velocity at finite baryon densities in the presence of a uniform external magnetic field. We can anticipate the main new results of our study: within the quasiparticle model, we study for the first time the polarization of dense strange quark matter in a strong magnetic background field, and we complete this investigation by the calculation of the squared speed of sound. The paper is outlined as follows. In Sec. II, we review the thermodynamically-consistent quasiparticle model with a chemical-potential-dependent bag constant in strong magnetic fields. In Sec. III, we present the numerical results and discussions of our calculations. Finally, a summary is given in Sec. IV.
-
Unlike the density-dependent mass model where the quark masses are density-dependent [74–78], in the quasiparticle model, the strong interactions between quarks are mimicked by arranging a chemical potential dependence of the quark masses. For the medium dependence, the effective quark mass used in this work was derived in the zero-momentum limit of the dispersion relation following from an effective quark propagator [68] by resuming one-loop self-energy diagrams in the hard dense loop approximation [79, 80]:
$ \begin{align} m_{i}^{*} =\frac{m_{i 0}}{2}+\sqrt{\frac{m_{i 0}^{2}}{4}+\frac{g^{2} \mu_{i}^{2}}{6 \pi^{2}}}, \end{align} $

(1) where
$ m_{i0} $ and$ \mu_i $ are respectively the current quark mass and chemical potential of quark flavor i.In Refs. [70, 81], the properties of strange quark matter with and without finite size effects are investigated in the quasiparticle model, in which the strong coupling is treated as a pure constant. However, it is well-known that the strong coupling g runs with the energy scale, and here we adopt the following phenomenological expression [82]
$ \begin{align} g^{2}= \frac{48 \pi^{2}}{29\ln \left(a \mu_{i}^{2}/\Lambda^{2}\right)}, \end{align} $

(2) where
$ a=0.8 $ , and Λ is the QCD scale parameter controlling the rate at which QCD coupling runs as a function of energy scale. In the vanishing current mass limit, Eq. (1) reduces to$ \begin{align} m_{i}^{*}=\frac{g \mu_{i}}{\sqrt{6} \pi}, \end{align} $

(3) which can be used as the effective masses for up and down quarks since their current masses are small compared to the strange quark. Note that since electrons do not participate in strong interactions, their masses keep constant as in the normal case.
To consider the effects of a strong magnetic field on the Landau quantization and the spin polarization of the strongly interacting quark matter, we need to know the energy spectrum of the spin-half particle in a strong magnetic field. Without loss of generality, we assume the external magnetic field along with the z-direction, i.e.,
$ {\boldsymbol{{\cal{B}}}}=B_m\hat{z} $ . In consequence, the energy spectrum of the spin-half charged particle can be obtained by solving the Dirac equation. We accordingly have$ \begin{align} \varepsilon_{i}=\sqrt{p_{z}^{2}+\bar{m}_{i, \nu}^{*2} }. \end{align} $

(4) Here
$ \bar{m}_{i, \nu}^{*}=\sqrt{m_{i}^{*2}+2 \nu |q_i| B_m} $ is the effective mass of particle i in the presence of an external magnetic field,$ p_z $ is the particle momentum in the z-direction,$ q_i $ is the electronic charge of particle i, and the Landau level ν is defined as [83, 84]$ \begin{align} \nu=l+\frac{1}{2}-\frac{\eta}{2}\frac{q_i}{|q_i|}, \end{align} $

(5) where l denotes the orbital angular momentum, and
$ \eta=\pm 1 $ represents the two eigenstates of the spin-half charged particle with "+1" for spin up and "-1" for spin down. Due to the Landau quantization, the integral over the momentum components perpendicular to the magnetic field become discrete. Consequently, we have$ \begin{align} \int \int \int {\rm d} p_{x} {\rm d} p_{y}{\rm d} p_{z} \rightarrow 2 \pi |q_i| B_{m} \sum_{\eta=\pm 1} \sum_{l}\int \text{d} p_{z}. \end{align} $

(6) Rewriting Eq. (4) in terms of the chemical potential, and defining the maximum
$ p_z $ as$ p_{z,F}=\sqrt{\mu_{i}^{2}-\bar{m}_{i, \nu}^{*2}} $ , we then have an upper limit for the Landau levels$ \begin{align} \nu \leq \nu_{i,\max } = \text{Int}\left[\frac{\mu_i^{2}-m_i^{*2}}{2|q_i| B_m}\right], \end{align} $

(7) due to the fact that the Fermi momenta
$ p_{z,F} $ must be real-valued quantities. In Eq. (7), the symbol$ \text{Int}[...] $ represents the floor of the enclosed quantity.At zero temperature, the quasiparticle contribution
$ \Omega_i\equiv\Omega_i(\mu_i,m_i^{*}) $ to the total thermodynamic potential density for magnetized quark matter is given by$ \begin{aligned}[b] \Omega_{i} =& -\frac{d_{i} |q_i| B_m}{4 \pi^{2}} \sum_{\eta=\pm 1} \sum_{l}\Bigg\{ \mu_{i} \sqrt{\mu_{i}^{ 2}-\bar{m}_{i, \nu}^{*2}}\\ &-\left.\bar{m}_{i, \nu}^{*2} \ln \left(\frac{\mu_{i}+\sqrt{\mu_{i}^{ 2}-\bar{m}_{i, \nu}^{*2}}}{\bar{m}_{i, \nu}^{*}}\right)\right\}, \end{aligned} $

(8) with the degenerate factor
$ d_i=1 $ for electrons and$ d_i=3 $ for quarks respectively. The pressure and energy density for magnetized SQM within the quasiparticle model are given by$ \begin{align} P=-\Omega-B^{*}, \end{align} $

(9) $ \begin{align} E=\Omega+\sum_{i} \mu_{i} n_{i}+B^{*}, \end{align} $

(10) where
$ \Omega\equiv\sum_i\Omega_i $ is the total thermodynamic potential density② containing a summation of all quasiparticle contributions in Eq. (8), while$ B^{*}\equiv \sum_iB_i(\mu_i,m_i^{*})+B_0 $ is the chemical potential dependence of the effective bag constant introduced to fulfill the thermodynamic self-consistency requirement [70].$ B_0 $ is the MIT bag constant, which is taken to be zero since it is not numerically relevant to our calculations. Note that there is no need to introduce an effective bag constant for electrons since they do not participate in the strong interactions and thus their mass is not dependent on the chemical potential. For a quasiparticle Fermi system the number density of the component i has the same form as the free-particle case in the presence of an external magnetic field, which is given by$ \begin{align} n_{i}=\frac{d_{i} |q_i| B_{m}}{2 \pi^{2}} \sum_{\eta=\pm 1} \sum_{l} \sqrt{\mu_{i}^{2}-\bar{m}_{i, \nu}^{*2} }. \end{align} $

(11) According to the fundamental differential equation of thermodynamics, the number density
$ n_i $ is obtained by taking the first derivative of the thermodynamic potential density with respect to the corresponding chemical potential$ \mu_i $ . Mathematically, this is equivalent to requiring$ \begin{align} n_{i}=-\left.\frac{\text{d} \Omega}{\text{d} \mu_{i}}\right|_{\mu_{j\neq i}} =-\frac{\partial \Omega_{i}}{\partial \mu_{i}}- \underbrace{\left[\frac{\partial \Omega_{i}}{\partial m_{i}^{*}} \frac{\text{d} m_{i}^{*}}{\text{d} \mu_{i}}+\frac{\partial B^{*}}{\partial \mu_{i}} \right]}_{=0}.\; \; \end{align} $

(12) In the above, the first term on the right hand side of the second equality is in fact equal to Eq. (11), while the vanishing of the second term is required to satisfy the thermodynamic consistency requirement of the quasiparticle model [73]. From Eq. (12), we have
$ \begin{align} \frac{\text{d} B^{*}}{\text{d} \mu_{i}} \frac{\text{d} \mu_{i}}{\text{d} m_{i}^{*}}=-\frac{\partial \Omega_{i}}{\partial m_{i}^{*}} \end{align} $

(13) or equivalently
$ B^{*} =-\frac{d_{i} |q_{i}| B_{m}}{2 \pi^{2}} \sum_{\eta=\pm 1} \sum_{l} \int_{\mu_{i}^{c}}^{\mu_{i}} m_{i}^{*} \frac{\text{d} m_{i}^{*} }{\text{d} \mu_{i}} $

$ \quad\quad\times \ln \Bigg(\frac{\mu_{i}+\sqrt{\mu_{i}^{2}-\bar{m}_{i, \nu}^{*2}}}{\bar{m}_{i, \nu}^{*}}\Bigg) \text{d} \mu_{i}. $

(14) To ensure the positive of the square root in Eq. (14), the lower limit of the integration over
$ \mu_i $ in Eq. (14) should satisfy$ \begin{align} \mu_{i}^{c 2}-\bar{m}_{i, \nu}^{*2} \geq 0. \end{align} $

(15) By using the effective quark mass in Eq. (1), the medium-dependent effective bag constant
$ B^{*} $ can be derived by numerical integration. -
In this section, we will present our results on the properties of various thermodynamic quantities in the presence of an external strong magnetic field at nonzero baryon densities. For stable SQM, β-equilibrium can be reached by the weak reactions
$ d, s \leftrightarrow u+e+\bar{v}_{e} $ and$ s+u \leftrightarrow u+d $ . Correspondingly, we have the following conditions for the relevant chemical potentials:$ \begin{align} \begin{cases} \mu_d=\mu_s\equiv \mu, \cr \mu_u+\mu_e=\mu. \end{cases} \end{align} $

(16) Here the chemical potential of neutrinos is set to zero because they can enter or leave the system freely. We also have the expressions of the baryon density
$ \begin{align} n_b=\frac{1}{3}(n_u+n_d+n_s), \end{align} $

(17) and the charge neutrality condition
$ \begin{align} \frac{2}{3}n_u-\frac{1}{3}n_d-\frac{1}{3}n_s-n_e=0, \end{align} $

(18) which has to be fulfilled for stable SQM presented in compact stars.
-
Strange stars are hypothetical objects consisting of stable SQM in the β-equilibrium condition. For a given baryon density, one can numerically solve the set of equations in (16), (17), and (18) to obtain the corresponding quark and electron chemical potentials. In Fig. 1, quark and electron chemical potentials are shown as functions of the baryon density at fixed
$ B_m $ . The blue dashed and green dotted curves correspond to$ \mu_u $ and μ with the same magnetic field strength$ B_m=10^{18} $ G, while the red and black solid curves represent the electron chemical potentials at two different magnetic field strengths,$ B_m=10^{17} $ G and$ B_m=10^{18} $ G, respectively. As can be seen from the figure, both$ \mu_u $ and μ monotonically increase with baryon density for fixed magnetic field strength. In both cases the electron chemical potential$ \mu_e $ first increases then decreases after reaching a maximum with increasing baryon density. The peaks for the electron chemical potential are approximately located at$ n_b\approx0.20\; \text{fm}^{-3} $ . The only difference of these two curves is the obvious oscillation shown by the solid black line with$ B_m=10^{18} $ G, an order of magnitude larger than the value$ B_m=10^{17} $ represented by the solid red line. As a minor comment, we notice that$ \mu_e $ experiences fluctuations for large values of$ B_m $ . These are due to the fact that electron density is fixed by the condition of electrical neutrality: at zero temperature and in the lowest Landau level approximation,$ n_e \propto eB_m\mu_e $ ; thus,$ \mu_e $ is sensitive to the behavior of the density of the quarks and in particular to their oscillations. However, the oscillations of$ \mu_e $ as well as those of the chemical potentials of the quarks are very tiny; see the scale on the right vertical axis in Fig. 1: they are of the order of a few MeV, therefore they are easy to visualize for$ \mu_e $ which is of the order of 20 MeV, but are invisible for the quarks since their chemical potentials are in the range$ 200\sim500 $ MeV.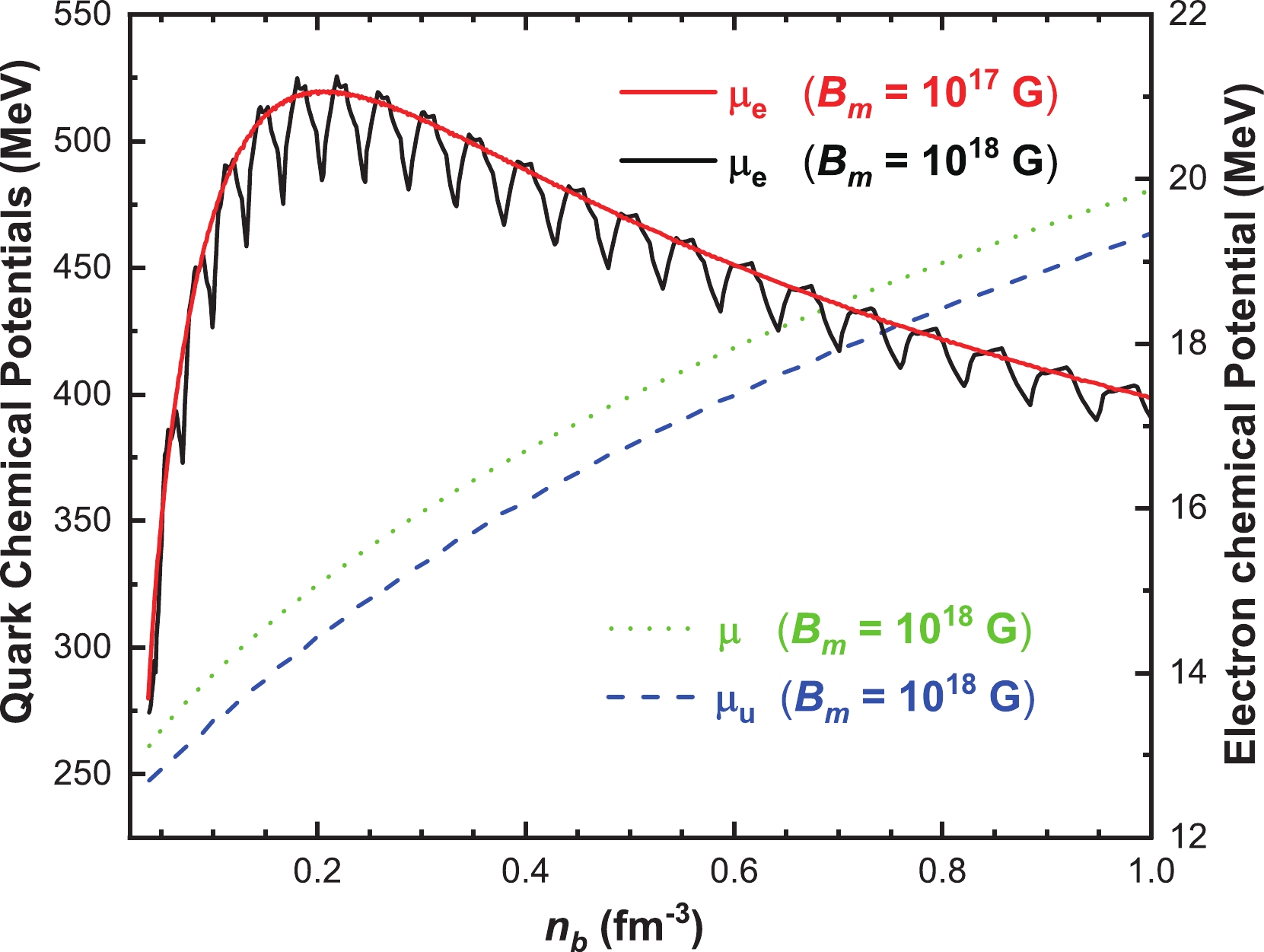
Figure 1. (color online) Quark and electron chemical potentials as functions of the baryon density for two different magnetic field strengths.
As well as the chemical potentials, the presence of a magnetic field also modifies the distribution of Landau levels. In Fig. 2, the maximum Landau levels for each component of SQM, i.e. up, down and strange quarks and electrons, are plotted as functions of the baryon density for two different magnetic field strengths. The red and black solid curves represent the cases with magnetic field strength
$ B_m=10^{17} $ G and$ B_m=10^{18} $ G, respectively. We observe that the curves, representing the maximum Landau levels of quarks, grow almost linearly with increasing density at fixed magnetic field strength. Owing to the strong suppression of$ \nu_{i,\text{max}} $ in strong magnetic fields, the slope of the black curves ($ B_m=10^{18} $ G) is much smaller than that of the red curves ($ B_m=10^{17} $ G). Moreover, at very low densities with fixed magnetic field strength, the inequalities$ \nu_{d,\text{max}}>\nu_{u,\text{max}}>\nu_{s,\text{max}} $ hold, while at relatively high density, we have$ \nu_{d,\text{max}}>\nu_{s,\text{max}}>\nu_{u,\text{max}} $ . This phenomenon can be understood because down and strange quarks share the same chemical potential μ, but the latter always has a larger effective mass due to the non-vanishing current mass$ m_{s0} $ , which automatically leads to$ \nu_{d,\text{max}}>\nu_{s,\text{max}} $ . On the other hand, the condition$ \mu_u<\mu\equiv\mu_s=\mu_d $ should be fulfilled for any density because of the consideration of β-equilibrium with the weak reactions$ d, s \leftrightarrow u+e+\bar{v}_{e} $ and$ s+u \leftrightarrow u+d $ . As a consequence,$ \nu_{d,\text{max}}>\nu_{u,\text{max}}>\nu_{s,\text{max}} $ holds at low densities owing to the large value of effective strange quark mass but small strange quark chemical potential in this region. However, as we increase the density, the numerator in Eq. (7) for the strange quark increases much faster than for the up quark, and at the same time$ \nu_{u,\text{max}} $ is always reduced by a factor of two compared to expression of$ \nu_{s,\text{max}} $ due to the ratio$ |q_u/q_s|=2 $ . It can be checked that as the density increases, the difference between these two maximal Landau levels grows and finally leads to$ \nu_{u,\text{max}}<\nu_{s,\text{max}} $ at high densities.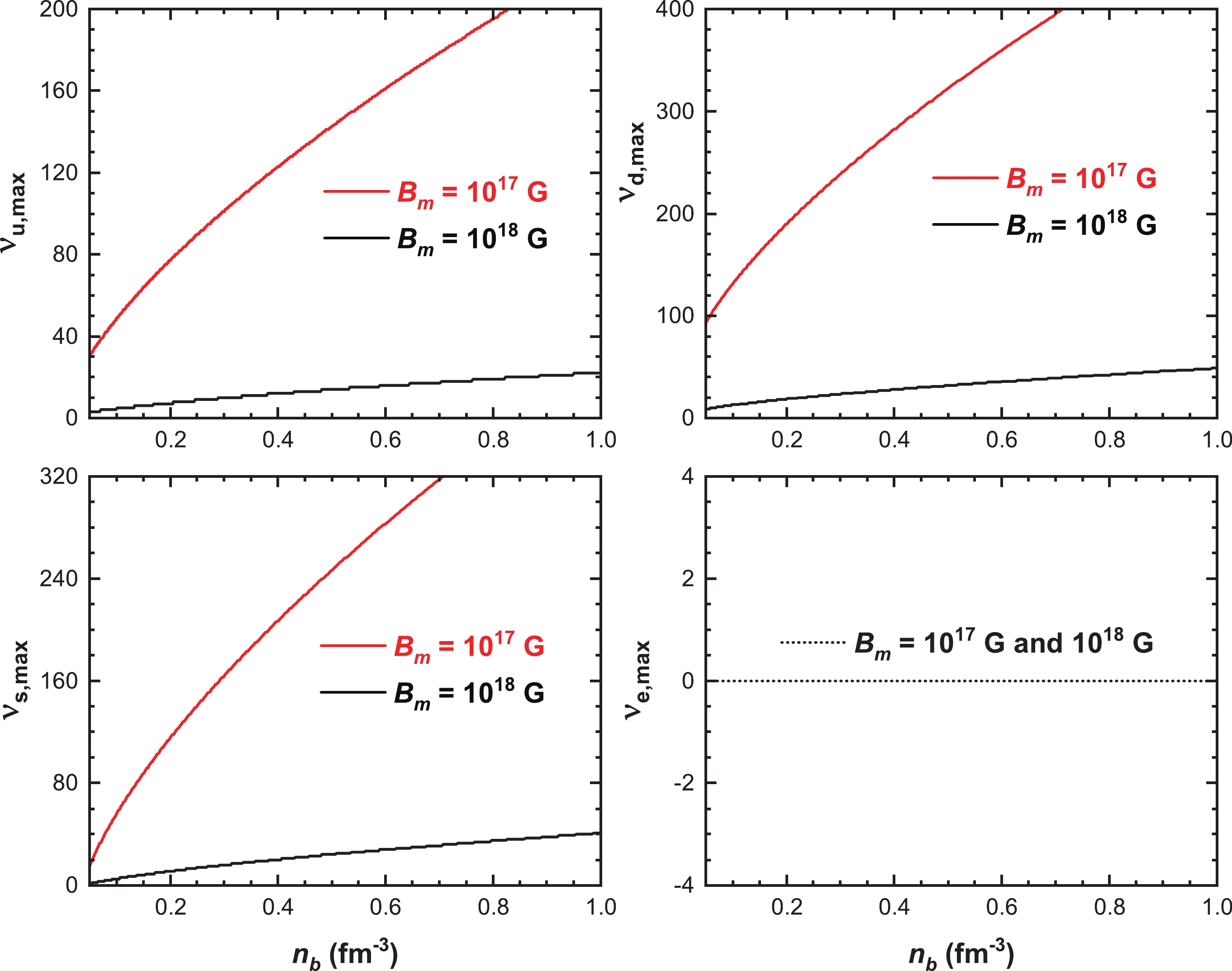
Figure 2. (color online) Maximum Landau levels for up, down and strange quarks, and electrons, changing with the baryon density.
For the two selected magnetic field strengths, i.e.,
$ B_m=10^{17} $ G and$ B_m=10^{18} $ G, the maximum Landau levels for electrons stay at zero since the corresponding electron chemical potentials are small, only a few tens of MeV, compared with the magnetic field strengths. In this case, only the lowest Landau level contributes to the thermodynamic quantities of magnetized SQM, which is also explicitly confirmed in Fig. 3. This particular shape for the density dependence of the electron chemical potential is responsible for the behavior of the relative spin polarization$ \Delta_e $ as shown in the two panels of Fig. 5. From Eq. (11), it is expected that the number density of electrons is completely determined by the behavior of the electron chemical potential$ \mu_e $ for a fixed magnetic field strength, namely,$ n_e $ also first increases and then decreases with increasing baryon density.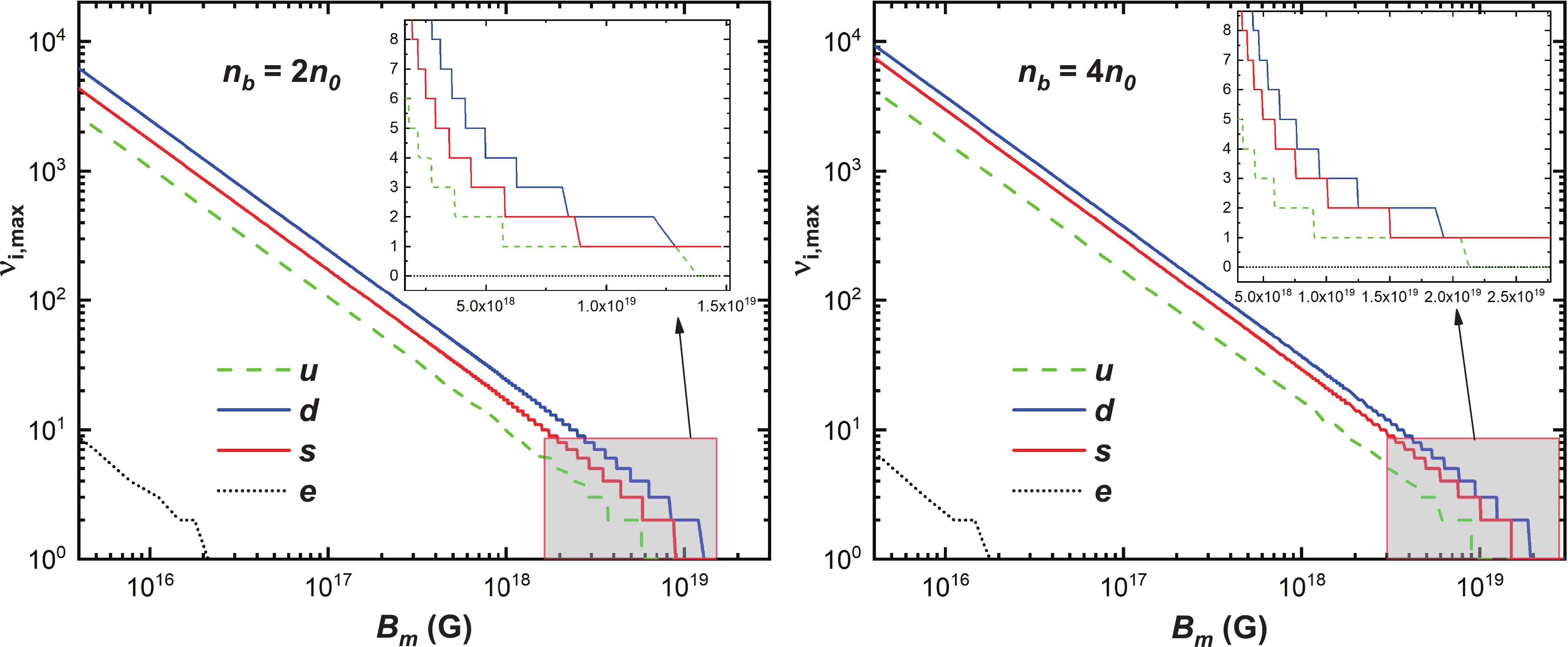
Figure 3. (color online) Maximum Landau levels for various charged particles as a function of magnetic field strength for
$ n_b=2n_0 $ (left panel) and$ n_b=4n_0 $ (right panel), where$ n_0=0.16\; \text{fm}^{-3} $ is the saturation nuclear density.In Fig. 3, we plot the maximum Landau levels for each component of β-equilibrium magnetized SQM as functions of the magnetic field strength at
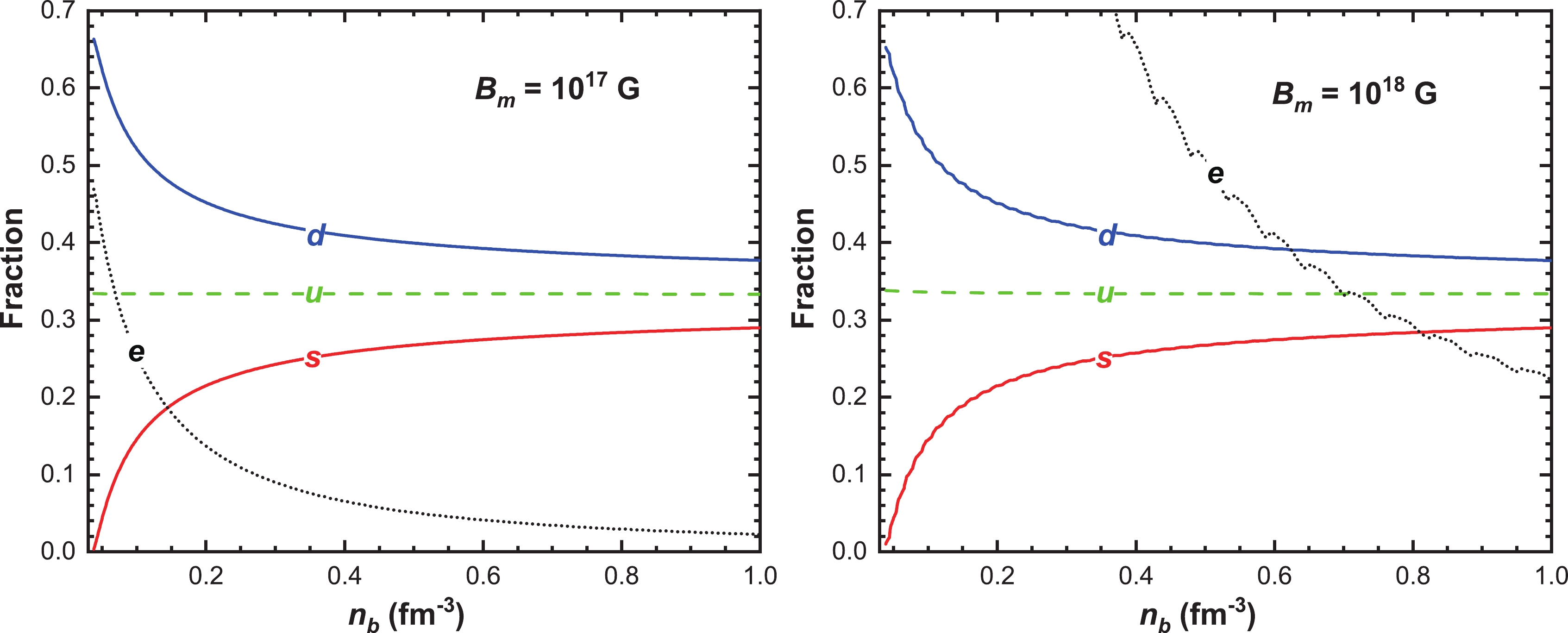
$ n_b=2n_0 $ (left panel) and$ n_b=4n_0 $ (right panel), where$ n_0=0.16\; \text{fm}^{-3} $ is the saturation density of normal nuclear matter. For the sake of convenience we use logarithmic scales to label both the vertical and horizonal axes. The electron maximum Landau level$ \nu_{e,\text{max}} $ , represented by the black dotted curve, decreases from a value about ten to one at around$ 1.8\times10^{16}\; \text{G} $ and$ 1.5\times10^{16}\; \text{G} $ in the left and right panels respectively. The maximum Landau levels for down, strange, and up quarks, which are denoted by the solid blue, solid red, and dashed green curves from right to left respectively, exhibit similar behavior: the curves decrease monotonously with increasing magnetic field strength and show obvious ladder-like shape at extremely large magnetic field strengths. Furthermore, it can be seen that the maximum Landau levels decrease almost linearly with the magnetic field strength, which agrees well with the Nambu–Jona-Lasinio finding of Ref. [85].In Fig. 4, we plot the quark fractions, i.e.
$ n_u/(3n_b) $ ,$ n_d/(3n_b) $ ,$ n_s/(3n_b) $ , and the$ 10^3 $ times electron fraction$ 1000n_e/(3n_b) $ , as functions of the baryon density at fixed magnetic field strength$ B_m=10^{17} $ G (left panel) and$ B_m=10^{18} $ G (right panel), respectively. One can see that the fraction of down and strange quarks decrease and increase respectively with increasing baryon density in both panels, while the fraction of up quarks stays almost constant in the considered range of the baryon density. The fractions of different quark flavors approach each other when the density is large enough. In addition, the fraction of electrons is very small and decreases with increasing density. Also, the oscillation of the electron fraction become more obvious for larger magnetic field strengths. -
From Eq. (11), one can easily deduce that in the presence of an external magnetic field the number density of each constituent of magnetized SQM has two contributions, corresponding to the particles with spin parallel and antiparallel to the magnetic field orientation respectively. To study the spin polarization of the magnetized SQM, we introduce the relative spin polarization for i-type particle as [86–88]
$ \begin{align} \Delta_{i}=\frac{n_{i}^{\uparrow}-n_{i}^{\downarrow}}{n_{i}^{\uparrow}+n_{i}^{\downarrow}}, \end{align} $

(19) where
$ n_{i}^{\uparrow} $ and$ n_{i}^{\downarrow} $ denote the number density of spin up and down i-type particles. When$ B_m=0 $ , we obviously have$ n_i^{\uparrow}=n_i^{\downarrow} $ and hence$ \Delta_{i}=0 $ . For nonzero external magnetic field, however, there is an upper value of the magnetic field$ B_m^{c,i} $ for which complete saturation of each constituent of the SQM occurs according to the expression$ n_i=n_i^{\uparrow}+n_i^{\downarrow} $ and Eq. (11). When the magnetic field reaches or exceeds the critical value$ B_m^{c,i} $ , from Eq. (5) the condition for each constituent particle$ \Delta_{i}=1 $ or$ \Delta_{i}=-1 $ is satisfied. The critical field value$ B_m^{c,i} $ saturates the system and aligns all the i-type particles parallel or antiparallel to the magnetic field depending on the electric charge of the particles. Note that, as deduced from the MIT bag model [89, 90] without taking into account the strong interactions between quarks, the inclusion of anomalous magnetic moment will further affect the properties of magnetized SQM and hence alert the values of$ B_m^{c,i} $ . This is beyond the scope of this work.In Fig. 5, we plot the relative spin polarization of each constituent of magnetized SQM as a function of the magnetic field strength, for two different baryon densities
$ n_b=2n_0 $ (left panel) and$ n_b=4n_0 $ (right panel). The curves from top to bottom correspond to$ \Delta_u $ (green dashed curve),$ \Delta_d $ (blue solid curve),$ \Delta_s $ (red dot-dashed curve), and$ \Delta_e $ (black dotted curve) in both panels. We observe that the curves in both panels show similar behaviors for each type of particle with increasing magnetic field strength. More specifically, the relative spin polarization of electrons$ \Delta_e $ begins to depart from zero at around$ 10^{15} $ G and the electrons become completely aligned antiparallel to the magnetic field at around$ 3.6\times10^{16} $ G and$ 3.0\times10^{16} $ G in the left and right panels, respectively. The relative spin polarization of quarks begins to depart from each other at around$ 3.0\times10^{17} $ G and this effect becomes notable after$ 10^{18} $ G. As shown in the left panel of Fig. 5,$ \Delta_u $ ,$ \Delta_s $ , and$ \Delta_d $ successively become completely saturated at the magnetic field strengths$ 1.3\times10^{19} $ ,$ 1.7\times10^{19} $ , and$ 2.5\times10^{19} $ G. A comparison of these two panels shows that for a larger baryon density the critical magnetic field$ B_m^{c,i} $ for quarks becomes larger, whereas the one for electrons does exactly the opposite. As stated in Sec. III A, this behavior can be explained by the density dependence of the quark and electron chemical potentials shown in Fig. 1. Namely, due to the monotonic behavior of quark chemical potentials as functions of the density, larger quark chemical potentials lead to larger maximum Landau levels and in turn to smaller absolute values of$ \Delta_{i} $ for quarks. However, for the two chosen baryon densities$ n_b=2n_0 $ and$ n_b=4n_0 $ , which are larger than the typical value of the location of the peak for electron chemical potential$ n_b\approx0.20\; \text{fm}^{-3} $ shown in Fig. 1, the electron chemical potential decreases with increasing$ n_b $ , which means that a larger baryon density$ n_b $ leads to a smaller maximum Landau level$ \nu_{e,\text{max}} $ and hence to a smaller absolute value of$ \Delta_e $ .Our study reveals that there is a narrow region, close to the critical field value where
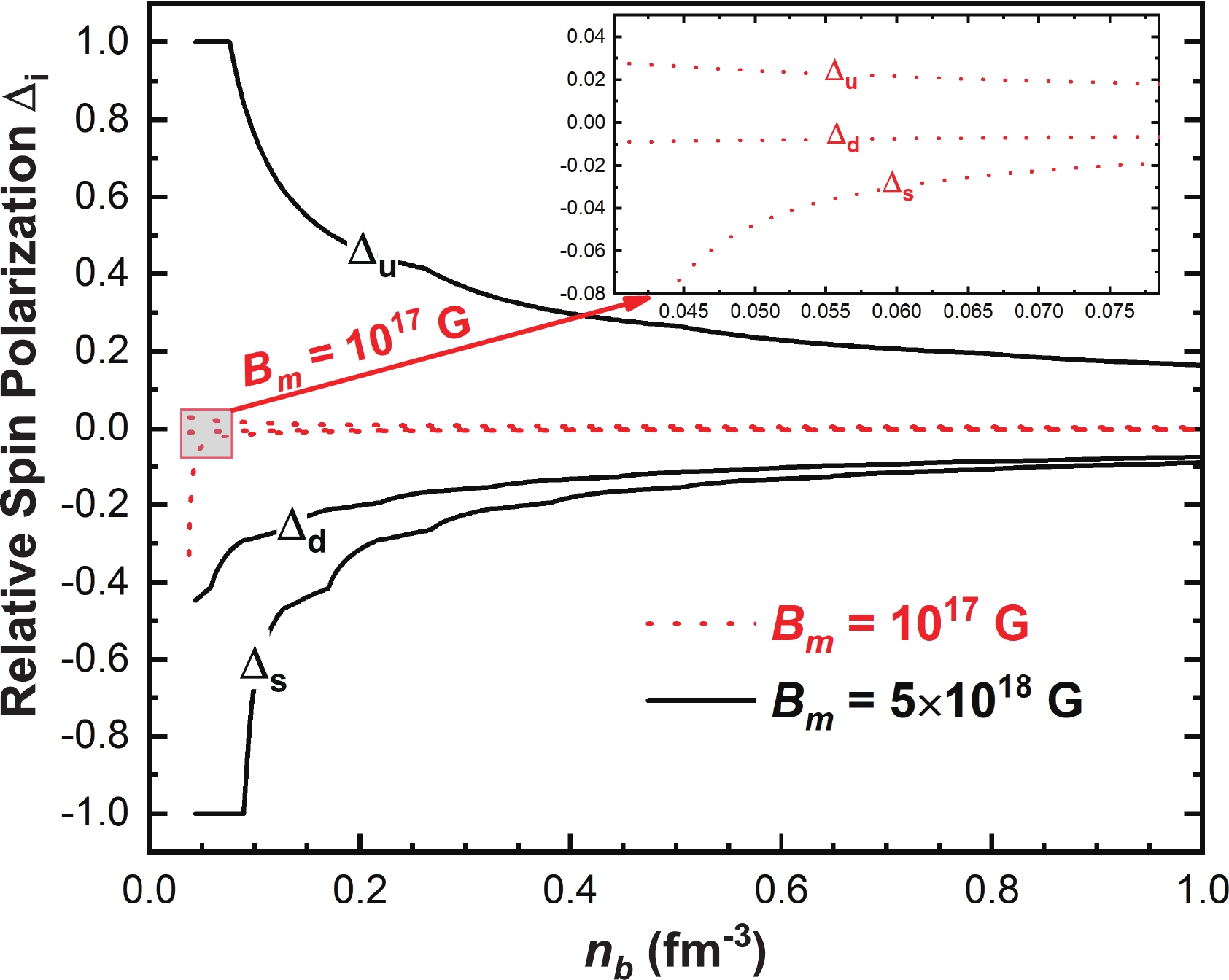
$ \Delta_u=-1 $ is reached, in which the β-equilibrium and charge neutrality conditions can not be fulfilled simultaneously. In other words, a negative solution for the electron chemical potential is found in this region [91]. When the magnetic field becomes larger, the charge neutrality condition is fulfilled again. Besides, one can also read from the figure that depending on the electric charge, the up quarks tend to polarize aligning spins with the magnetic field orientation, whereas the particles with negative electric charges like electrons, down and strange quarks do the opposite, which is consistent with the finding in Refs. [86, 87].In Fig. 6, we display the variation of the relative spin polarizations with density for up, down, and strange quarks under the β-equilibrium condition at two representative magnetic field strengths
$ B_m= 10^{17} $ G and$ B_m= $ $ 5\times10^{18} $ G. For the magnetic field strength$ B_m= 10^{17} $ G, denoted by the red dotted curves, the number densities with spin up and down almost coincide with each other in the whole considered density range. However for the magnetic field strength$ B_m=5\times10^{18} $ G, denoted by the black solid curves, all the curves largely deviate from zero at low densities and gradually tend to zero with increasing baryon density. As we have shown in Figs. 2 and 3, the maximum Landau levels of quarks increase with the increase of the baryon density but decrease with increasing magnetic field strength. As a consequence, the characteristic behavior of the occupation of the Landau levels responsible for that although the magnetic field effects enhance the spin polarization, the finite baryon density effect tends to reduce the difference of spin polarization for magnetized SQM. -
The strength of interaction and the stiffness of the equation of state can be measured by the sound velocity. In Fig. 7, we present the sound velocity squared
$ V_s^2 $ as a function of the baryon density, which is determined by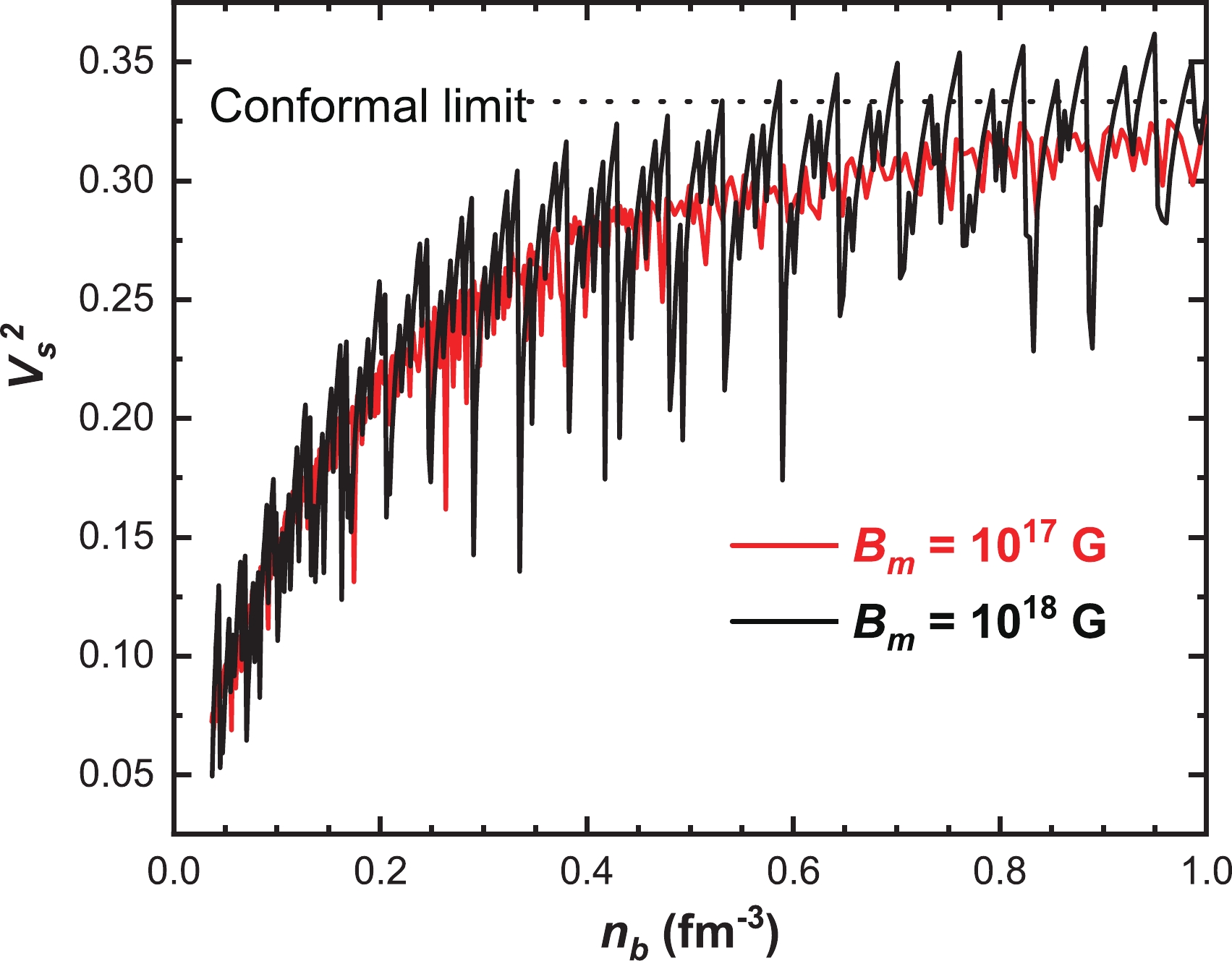
Figure 7. (color online) Sound velocity of magnetized cold quark matter as a function of the baryon density for different values of magnetic fields. The horizontal line represents the conformal limit
$ V_s^2=1/3 $ .$ \begin{align} V_s^2= \frac{\text{d} P}{\text{d} E}. \end{align} $

(20) The red and black solid curves correspond to
$ B_m=10^{17} $ G and$ B_m=10^{18} $ G respectively, while the black dashed line represents the conformal limit. It is found that in both cases, the sound velocity increases from small values with increasing baryon density and asymptotically approaches the conformal limit$ V_s^2=1/3 $ at high densities. The only difference is that the curve with a stronger magnetic field shows a more obvious oscillation. Except for the oscillation, the density behavior of sound velocity in the present work is qualitatively the same as for the zero magnetic field case [70]. Since the two curves approach the conformal limit from below, the sound velocity of magnetized SQM also fulfills the causality limit$ V_s^2<1 $ . It is worth mentioning that to explain recent cosmological data like large masses of pulsars with a mass of about two solar masses and tidal deformability observational data, there have been many discussions suggesting that the sound velocity of dense matter should be larger than the conformal limit$ V_s^2=1/3 $ , see e.g. Refs. [92–94]. Such statements have been confirmed both by the model calculations [95] and statistical analysis [96]. However, we should emphasize that such kind of calculations are mostly done by assuming that the compact stars are neutron stars or hybrid stars undergoing a phase transition [97]. -
We have explored the behaviors of various thermodynamic quantities of the magnetized SQM, with consideration of β-equilibrium and charge neutrality conditions, in response to the baryon density as well as to the magnetic field strength at nonzero chemical potentials, within the framework of the quasiparticle model. The quark chemical potentials are found to increase with the increment of baryon density at a certain magnetic field strength, which is the same behavior as for zero magnetic field.
As the magnetic field increases, the relative spin polarizations of electrons and quarks begin to depart from zero at
$ {\cal{O}}(10^{15}\; \text{G}) $ and$ {\cal{O}}(10^{17}\; \text{G}) $ , and the corresponding absolute values become one at$ {\cal{O}}(10^{16}\; \text{G}) $ and$ {\cal{O}}(10^{19}\; \text{G}) $ , respectively. In particular, for higher values of the baryon density the critical magnetic field strengths for$ |\Delta_{i=u,d,s}|=1 $ move to larger values of$ B_m $ , while the value for electrons does either the opposite or the same, depending on the location of the corresponding electron chemical potential as shown in Fig. 1. Namely, a smaller value of$ \mu_e $ or$ n_e $ leads to a larger$ |\Delta_e| $ and in turn to a smaller critical magnetic field when$ \Delta_e=-1 $ is satisfied. Increasing the baryon density or the magnetic field affects the net polarization of quarks differently: this is easy to understand in terms of the occupation of the Landau levels, see Eq. (7). In fact, from that equation we see that increasing the chemical potential while keeping$ B_m $ fixed results in a higher number of occupied Landau levels, thus reducing the polarization. On the other hand, increasing$ B_m $ while keeping the chemical potential fixed results in the lowering of the number of occupied Landau levels, hence leading to the increase of the net polarization of strange quark matter. Thus, one can conclude that, as a consequence of the occupation of Landau levels, in contrast to the finite baryon density effect which reduces the absolute value of relative spin polarization, the magnetic field effect leads to an enhancement of spin polarization of the magnetized SQM.We have analyzed, for the first time within the quasiparticle model, the polarization of strange quark matter in the background of a strong magnetic field; moreover, we have also computed the squared speed of sound. Compared to the zero-magnetic field case, the sound velocity in an external magnetic field shows an obvious oscillation with increasing density, especially for the curve with a stronger magnetic field. The sound velocity, in addition to the visible oscillation phenomena, grows with increasing density and approaches the conformal limit
$ V_s^2=1/3 $ at high densities from below.
Landau quantization and spin polarization of cold magnetized quark matter
- Received Date: 2022-02-12
- Available Online: 2022-06-15
Abstract: The magnetic field and density behaviors of various thermodynamic quantities of strange quark matter under compact star conditions are investigated in the framework of the thermodynamically self-consistent quasiparticle model. For individual species, a larger number density


 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: